Question
Question: A long straight metal rod has a very long hole of radius \('a'\) drilled parallel to the rod axis as...
A long straight metal rod has a very long hole of radius ′a′ drilled parallel to the rod axis as shown in the figure. If the rod carries a current ′I′. Find the magnetic induction on the axis of the hole, where OC=c:
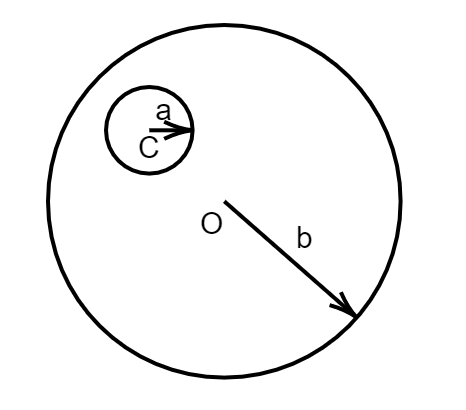
A. π(b2−c2)μ0Ic
B. 2π(b2−c2)μ0Ic
C. 2πcμ0I(b2−c2)
D. 2πa2b2μ0Ic
Solution
To solve this question, we will use Ampere’s circuital law. According to the Ampere’s circuital law, the magnetic field is related to the current flowing in the conductor. The law states that the integral value of the magnetic field density along an imaginary path is equal to the product of permeability of the free space and the current enclosed by that path.
Complete answer:
First let us apply the Ampere’s circuital law, assuming a circular Gaussian surface of radius c. So, from the Ampere’s circuital law we get:
∮B⋅dl=μ0I
Here, I is the enclosed circuit in the circular Gaussian surface of radius c and its value will be:
I=J⋅πc2
Here, J is the current flowing per unit cross-sectional area. Current density of the rod if it did not have a cavity, will be as follows:
J=πb2I
Since the metal rod has a cavity of radius a, hence the resulting cross-sectional area will be the cross-sectional area of the rod subtracted by the cross-sectional area of the cavity. Thus, and its value will be:
J=πb2−πa2I
Substituting these values in the Ampere’s circuital law we get:
∮B⋅dl=μ0πb2−πa2I⋅πc2B∮dl=μ0πb2−πa2I⋅πc2
On calculating the line integral, we will get the following equation:
B(2πc)=μ0πb2−πa2I⋅πc2⇒B=μ0(2πc)(πb2−πa2)I⋅πc2∴B=2π(b2−a2)μ0Ic2
Thus, the value of magnetic induction on the axis of the hole, where OC=c is 2π(b2−c2)μ0Ic.
So, the correct answer is “Option B”.
Note: One thing needs to be remembered that the Ampere circuital law as well as the Gauss law has to be applied to a body in which the flow of current is distributed symmetrically. The given problem fulfils this condition; hence we could use both Ampere’s circuital law and Gauss law to solve this problem.
