Question

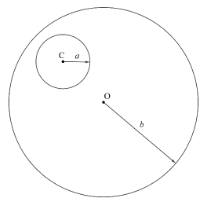
A long straight metal rod has a very long hole of radius $a$ drilled parallel to the rod axis as shown in the figure. If the rod carries a current $I$ , find the value magnetic induction on the axis of the hole, where $OC=c$

Answer 1

To find the magnetic induction on the axis of the hole, we need to use Ampere’s Circuital law, where the current enclosed in the Gaussian surface can be calculated by finding the current per area and multiplying with the area of the Gaussian surface.

Complete answer:
Here, we are given a long rod of radius $a$ in which the current passes through the axis of the rod.
A hole is drilled at a distance $c$ from the center of the rod of radius $b$ .
To find the magnetic induction at the axis of the hole, we can use Ampere’s circuital law.
$\oint{Bdl={{\mu }_{0}}{{I}_{enclosed}}}$
We can find the enclosed current by considering a Gaussian surface with center at $O$ and radius as the distance $c$ as shown in the figure.

As there is a hole drilled in the rod, to find the current, we need to find the current density that is defined as the total current per unit area.
$\therefore$ Current Density = $\dfrac{I}{\pi {{a}^{2}}-\pi {{b}^{2}}}$ , because the total area is the area of the rod without the area of the hole.
Now, the current enclosed by the Gaussian surface can be calculated as,
$\therefore {{I}_{enclosed}}=\dfrac{I}{\pi {{a}^{2}}-\pi {{b}^{2}}}\times \pi {{c}^{2}}$
Now, for Ampere’s circuital law, the line integral is the perimeter of the Gaussian surface.
$\therefore \oint{dl}=2\pi c$
Now, substituting these values in the equation of Ampere’s Circuital law,
$\therefore B\left( 2\pi c \right)={{\mu }_{0}}\left( \dfrac{I}{\pi {{a}^{2}}-\pi {{b}^{2}}}\times \pi {{c}^{2}} \right)$
$\therefore B=\dfrac{{{\mu }_{0}}}{\left( 2\pi c \right)}\left( \dfrac{I}{\pi {{a}^{2}}-\pi {{b}^{2}}}\times \pi {{c}^{2}} \right)$
Canceling the common part,
$\therefore B=\dfrac{{{\mu }_{0}}}{2\pi }\dfrac{Ic}{\left( {{a}^{2}}-{{b}^{2}} \right)}$
This is the magnetic induction at the axis of the hole.

Note:
Here, if the Gaussian surface was taken with center at $C$ and the same radius as the distance between the axis of wire and axis of the hole, the value of current at the axis of the hole will be correct, but the concept is wrong because the formula is used when the current is flowing at the center and the magnetic field is to be found at the perimeter of the surface, while here the case will be inverse. Hence, even though the correct answer is obtained the method will be wrong.