Question

A long, straight, hollow conductor (tube) carrying a current has two sections $A$and $C$ of unequal cross sections joined by a conical section $B.{\text{ }}1,2and{\text{ }}3.$Are points on a line parallel to the axis of the conductor. The magnetic fields at $1,2,{\text{ }}and{\text{ }}3.$Then,

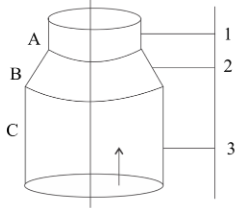
(A) ${B_1} = {B_2} = {B_3}$
(B) ${B_1} = {B_2} \ne {B_3}$
(C) ${B_1} < {B_2} < {B_3}$
(D) ${B_2}$ Can not be found unless the dimension of the select $B$are known

Answer 1

In order to solve this question,we must have knowledge about Ampere’s circuital law $\int {B.dl} = {\mu _0}I$. We have to take distance from the axis. $I$ remains the same for all portions.

Complete step by step answer:
We need to find the magnetic field outside a thick conductor, we need to consider the current that may be assumed to flow along the axis. As point $1,2{\text{ }}and{\text{ }}3$ is equidistant from the axis,
${B_1} = {B_2} = {B_3}$
So, by using ampere’s circuital law,
$\int {B.dl} = {\mu _0}I$

$$B.l = {\mu _0}I \\\ B.\left( {2\pi r} \right) = {\mu _0}I \\\ {B_1} = \dfrac{{{\mu _0}I}}{{2\pi r}} \\\ {B_2} = \dfrac{{{\mu _0}I}}{{2\pi r}} \\\ {B_3} = \dfrac{{{\mu _0}I}}{{2\pi r}} \\\$$

Since the distance from the axis to the point $1,{\text{ }}2,{\text{ }}3$ are same and the current $I$ through the tube is same so,
The magnetic field will remain the same in three-point $1,2and{\text{ }}3.$ and, for this exact reason, the answer will be.
${B_1} = {B_2} = {B_3}$
And its direction is perpendicular to the wire and is in the direction the fingers of your right hand would curl if you wrapped them around the wire with your thumb in the direction of the current. So, the direction of the magnetic field in this case is from the side with alphabets to the side with numbers. That is an anticlockwise direction.
The correct answer is $\left( A \right).$

Note: We should take the distance from the axis not from the edge or surface of the tube. If we take distance from the surface Option $\left( C \right)$ will be the answer which is not correct.