Question
Question: A long insulated copper wire is closely wound as a spiral of 'N' turns. The spiral has an inner radi...
A long insulated copper wire is closely wound as a spiral of 'N' turns. The spiral has an inner radius ‘a' and an outer radius ′b′. The spiral lies in the X−Y plane and a steady current 'I' flows through the wire. The Z-component of the magnetic field at the center of the spiral is :
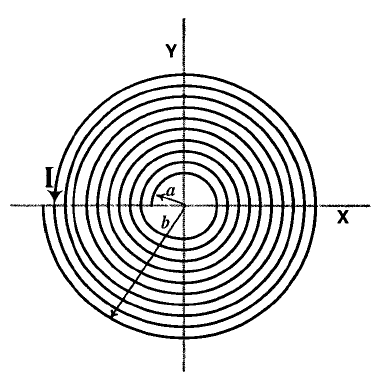
Solution
In this question, first we assume an elementary ring of radius r and thickness ‘dr’ and then find the number of turns in this elementary ring . After this we will find the magnetic field at the centre O. To find the magnetic field due to the whole spiral, we will integrate it from a to b.
Complete answer:
Let us consider an elementary ring of radius r and thickness dr in which current I is flowing.
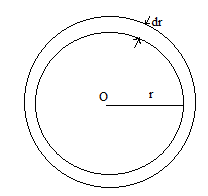
Number of turns in this elementary ring dN =b−aNdr
We know that magnetic field at the centre of a ring is given by:
B=2rμ0NI
Where,
μ0 is permeability of free space.
N is the number of terms.
I is currently flowing.
r is the radius of the ring.
Thus magnetic field at the centre O due to this ring dB=2rμ0dNI
Putting the value of dN, we get:
dB=2(b−a)rμ0NIdr
To get the net magnetic field at the centre of the spiral , we will integrate the above equation from ‘a’ to ‘b’.
0∫BdB =a∫b2(b−a)rμ0NIdr=2(b−a)μ0NIa∫brdr=2(b−a)μ0NI[lnr]ab
⇒B=2(b−a)μ0NIlnab
Therefore, the required magnetic field is ⇒B=2(b−a)μ0NIlnab
Note:
In this question, you should know how to calculate the magnetic field in the centre of the circular wire. The direction of the magnetic field in this case is given by right hand thumb rule. You should know the Biot-savart law which is used to calculate the magnetic field. The magnitude of magnetic field is given by:
dB=4πμ0r2Idlsinθ
