Solveeit Logo
Login

Question

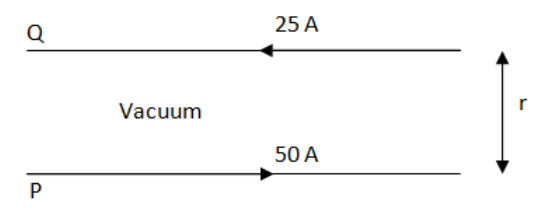
Question: A long horizontal wire P carries a current of 50 A. It is rigidly fixed. Another wire Q is placed di...

A long horizontal wire P carries a current of 50 A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in Figure. The weight per unit length of the wire Q is 0.025Nm−10.025N{m^{ - 1}} and it carries a current of 25 A. Find the distance 'r' of the wire Q from the wire P so that the wire Q remains at rest.

Explanation

Solution

Hint- In order to solve this question we will use the basic concept that the wire Q to be in equilibrium, F=mg where F, is the repel force acting on the wire Q due to P and mg is the weight of wire Q.

Formula used- weight=m(mass per unit length)×l(length),F=μ0I1I2l2πr{\text{weight}} = m\left( {{\text{mass per unit length}}} \right) \times l\left( {{\text{length}}} \right),F = \dfrac{{{\mu _0}{I_1}{I_2}l}}{{2\pi r}}.

Complete step-by-step solution -
Let the length of the given wire Q is 1 m
⇒l=1m\Rightarrow l = 1m
So the weight of wire Q
⇒weight=m(mass per unit length)×l(length) =0.025Nm−1×1m =0.025N.........(1)  \Rightarrow {\text{weight}} = m\left( {{\text{mass per unit length}}} \right) \times l\left( {{\text{length}}} \right) \\\ = 0.025N{m^{ - 1}} \times 1m \\\ = 0.025N.........(1) \\\
Since the current in both the wires is flowing in opposite directions, so both wires will repel each other.
Force acting on the wire Q due to P,
F=μ0I1I2l2πrF = \dfrac{{{\mu _0}{I_1}{I_2}l}}{{2\pi r}}
Substitute the value of both the current and length of wire, we get

∵F=μ0I1I2l2πr ⇒F=4π×10−7×50×25×12π×r ⇒F=25×10−5rN.............(2)  \because F = \dfrac{{{\mu _0}{I_1}{I_2}l}}{{2\pi r}} \\\ \Rightarrow F = \dfrac{{4\pi \times {{10}^{ - 7}} \times 50 \times 25 \times 1}}{{2\pi \times r}} \\\ \Rightarrow F = \dfrac{{25 \times {{10}^{ - 5}}}}{r}N.............(2) \\\

For the wire Q to be in equilibrium,
F=mgF = mg
Let us compare both the force as given in the problem to find the value of r
So equating equation (1) and equation (2) we get:
⇒25×10−5rN=0.025N\Rightarrow \dfrac{{25 \times {{10}^{ - 5}}}}{r}N = 0.025N
Let us solve the equation to find the value of r
⇒r=25×10−50.025 ⇒r=0.01m ⇒r=1cm  \Rightarrow r = \dfrac{{25 \times {{10}^{ - 5}}}}{{0.025}} \\\ \Rightarrow r = 0.01m \\\ \Rightarrow r = 1cm \\\
Hence, the distance 'r' of the wire Q from the wire P so that the wire Q remains at rest is 1cm.

Note- Fl\dfrac{F}{l} is the force per unit length between two parallel currents I1{I_1} and I2{I_2} separated by a distance r. The force is desirable if the currents are in the same direction and if they are in opposite directions they are repulsive. During electric arcs and plasmas, this force is responsible for the pinch effect. Volume is the measure of the volume of matter that comprises it, while Weight is the measure of the force of gravity on an object.