Question
Question: A long horizontal mirror is next to a vertical screen (see figure). Parallel light rays are falling ...
A long horizontal mirror is next to a vertical screen (see figure). Parallel light rays are falling on the mirror at an angle α from the vertical. If a vertical object of height h is kept on the mirror at a distance d>htanα, the length of the shadow of the object on the screen would be.
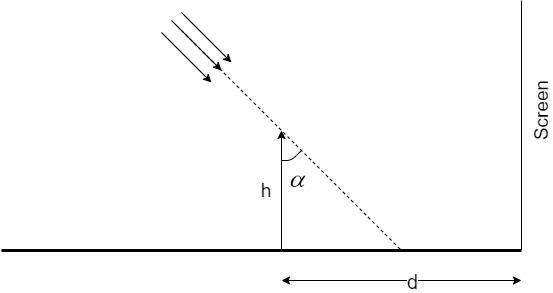
A. 2h
B. htanα
C. h
D. 4h
Solution
To solve this problem, we have to understand two important concepts and apply them in our problem: i) Law of reflection: The incident angle is equal to the reflected angle. ∠i=∠r
ii) The trigonometric ratio, tanθ is the ratio of the opposite side of the angle and its adjacent side. tanθ=AdjacentOpposite
Complete step by step answer:
The law of reflection states that the incident angle is equal to the reflected angle.
The object of height h is placed on the mirror. The shadow of the object falls on the mirror and the same shadow is reflected back on the screen
The corresponding geometry for the same is given in this figure:
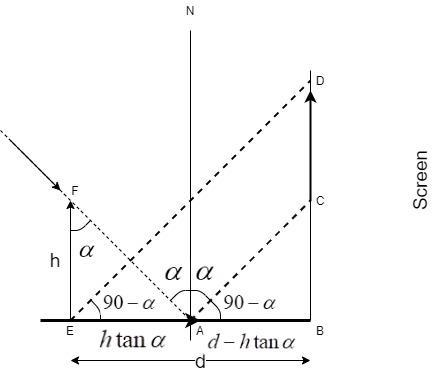
Let us understand the formation of the above geometry in detail.
When the object shadow falls on the mirror at the points A and E, it undergoes a reflection on the plane mirror and an image CD is formed on the screen.
At point A, we have a normal N. The angle made by the ray FA is equal to α since the lines EE and AN are parallel lines and AF is the transverse line, which makes the angles AFE and FAN alternate angles which are equal.
At point A, the incident angle is equal to α. Hence, the reflection angle NAD should also be equal to α by the law of the reflection.
Since N is the normal, the angle NAB being equal to 90, the angle CAB = 90−α
Since AC is parallel to ED, ∠DEB=∠CAB=90−α∵ corresponding angles.
In the triangle AEF,
tanα=AdjacentOpposite=EFAE=hAE
Thus, AE=htanα
Given that, AE + AB = d
AB=d−AE=d−htanα
To calculate the length of the shadow, we need to consider two triangles ABC and EBD to calculate the value of the length CD which is our required value.
In triangle ABC,
tan(90−α)=ABBC=d−htanαBC
The trigonometrical identity equal to tan(90−θ) is equal to another identity called cotθ, where –
cotθ=tanθ1
Hence,
cotα=d−htanαBC
In triangle EBD,
tan(90−α)=EBBD=dBD
The trigonometrical identity equal to tan(90−θ) is equal to another identity called cotθ, where –
cotθ=tanθ1
Hence,
cotα=dBD
By equating the values of cotα in the above triangles,
d−htanαBC=dBD
⇒BC×d=BD×(d−htanα)
⇒BC×d=BD×d−BD×htanα
⇒BD×htanα=d(BD−BC)
The required length, CD=BD−BC
Substituting the value of CD and the value of BC=(d−htanα)(cotα), we get –
(CD+BC)htanα=d×CD
(CD+cotα(d−htanα))htanα=d×CD
⇒CD(htanα)+hcotαtanα(d−htanα)=d×CD
Since cotα=tanα1
cotαtanα=1
Thus,
⇒CD(htanα)+h(d−htanα)=d×CD
⇒CD(htanα−d)=h(htanα−d)
⇒CD=(htanα−d)h(htanα−d)=h
Hence, the length of the shadow on the screen, CD = h
Hence, the correct option is Option C.
Note: In this answer, the concept of alternate and corresponding angles are directly applied here. Let us briefly understand them.
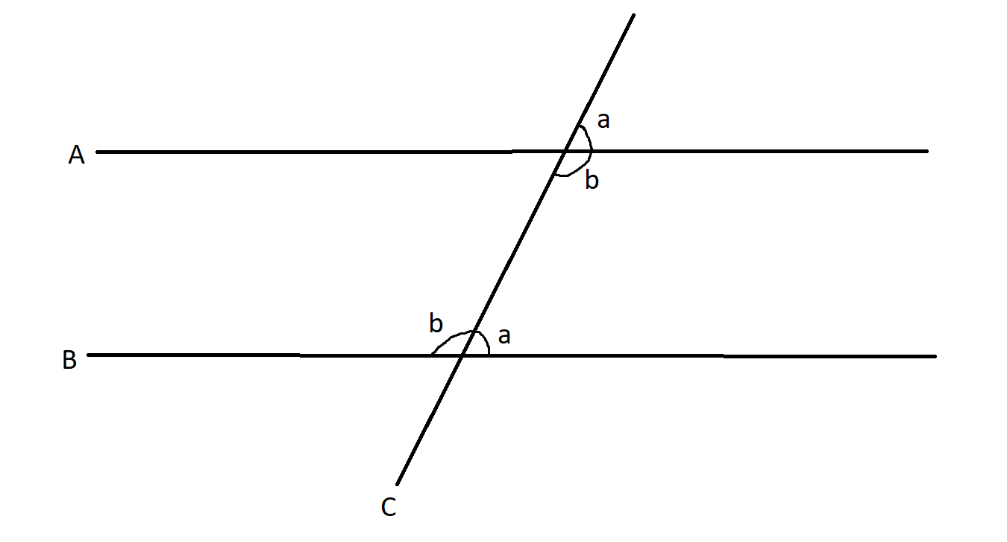
A and B are two parallel lines and the line C which intercepts them at an angle is called the transverse line. When a transverse line intercepts the parallel lines, we get several sets of angles.
Here, angles a are called corresponding angle pair and angles b are called alternate angle pair. The relation between them is a+b=180∘
