Question
Question: A long cylindrical volume contains a uniformly distributed charge of density \(\rho\). Find the elec...
A long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at point P inside the cylindrical volume at a distance x from its axis.
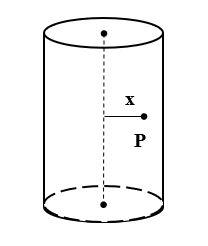
Solution
To answer this question, initially, find the charge on the cylinder. Charge can be calculated by taking the product of volume charge density and volume of the cylinder. Then, use the integral form of Gauss law for volume charge density. Substitute the values and calculate the electric field at point P inside the cylindrical volume.
Formula used:
Q=ρV
∮E.ds=ϵ0Q
Complete step by step answer:
Given: Volume charge density =ρ
Let the height of the cylinder be h
Charge on the cylinder is given by,
Q=ρV
Where, V is the volume of the cylinder
Substituting values in above equation we get,
Q=ρ×4πx2h
According to gauss law,
∮E.ds=ϵ0Q
∴E=dx×ϵ0Q
Substituting the values in above equation we get,
⇒E=2πxh×ϵ0ρ×4πx2h
∴E=2ϵ0ρx
Hence, the electric field at point P inside the cylinder is 2ϵ0ρx.
Note:
To answer these types of questions, students should remember the basic laws like Gauss law. There are two forms of Gauss law: integral form and differential form. Integral form of Gauss law is given by,
∮E.ds=ϵ0Q
Differential form is given by,
∇.E=ϵ0ρ
Gauss law is a restatement of Coulomb's law. If we apply the Gauss law to a point charge, then we'll get back the Coulomb's law.
