Question
Question: A long conducting wire carrying a current 1 is bent at \({{120}^{o}}\)(see figure). The magnetic fie...
A long conducting wire carrying a current 1 is bent at 120o(see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is (μ0 is the permeability of free space)
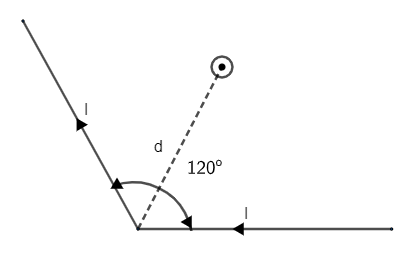
Solution
To measure the magnetic field at point P then first we have to take a single wire as two different from bend point then we have to measure perpendicular distance of point P from the both wire. Then by substituting this value in the magnetic field formula we can get the total magnetic field at point P.
Formula used:
B=4πdμ0I(sinθ1+sinθ2)
Complete answer:
First we will draw a perpendicular line from the point P on the both parts of the wire as shown in the figure.
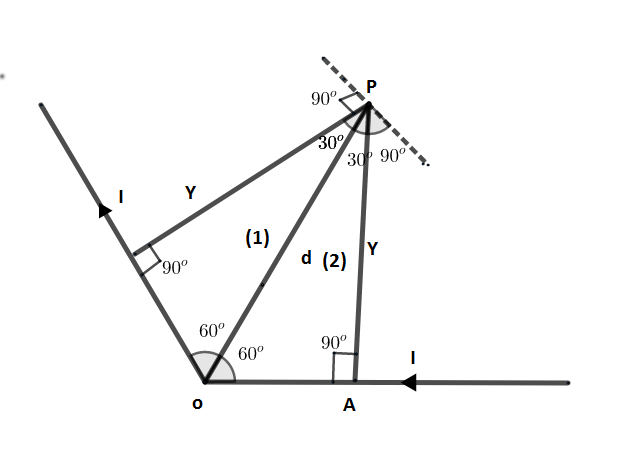
Consider now by using geometry of the triangle as shown in the figure.
As we can see that the angle of the both the triangles are the same, therefore both triangles will have same values of the side.
Therefore from the triangle OPA
sin60o=dY
Where, Y = perpendicular distance from the wire to the point P.
Y=2d3...(1)
Now formula for magnetic field,
B=4πYμ0I
Where,μ0= permittivity of free space.
I = current flowing in the wire.
θ1,θ2= angles a side of a perpendicular line.
For the triangle 1,
B1=4πYμ0I(sin30o+sin90o).....(2)
Substitute value of Y in the equation (2)
