Question

A long charged cylinder of linear density $+ {\lambda _1}$ is surrounded by a hollow coaxial conducting cylinder of linear charge density $- {\lambda _2}$ use Gauss’s law to obtain expressions for the electric field at a point
(i) in the space between the cylinders and
(ii) outside the cylinders

Answer 1

In order to solve this question we need to understand definition of gauss law which states that flux enclosed by a closed surface is equal to net charge contained divided by ${\varepsilon _0}$ and flux is equal to dot product of area vector and electric field vector. Linear charge density is defined as the charge stored on a cylinder per unit length of cylinder.

Complete step by step answer:
Before solving it is clear that the electric field from a line charge is always perpendicular to length. Area vector direction is the normal direction of surface. Since we know the area vector of the disc part of the cylinder points upward but the electric field points in perpendicular direction so there is no net flux through this surface as flux is a dot product between electric field and area vector.

Whereas from the curved part of the cylinder both electric field and area vector points in the same direction so flux through the surface is non zero.Flux is given by,
$\phi = \int {\vec E.d\vec s = \int {Eds} }$
So we know the electric field is uniform throughout the curved surface so we can take it outside integration.So flux is,
$\phi = E\int {ds}$

(i) So for first part consider a cylinder of radius ${r_1}$ in between two cylinder known as Gaussian cylinder

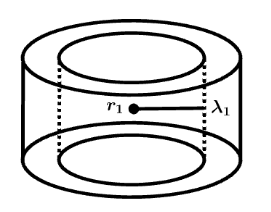
So net charge enclosed by this surface is $q = {\lambda _1}h$ where height of cylinder is $h$
So flux enclosed is given by $\phi = E\int {ds = E(2\pi {r_1}h)}$ as $\int {ds = 2\pi {r_1}h}$
So from gauss law $\phi = \dfrac{q}{{{\varepsilon _0}}}$
Putting values we get,
$E(2\pi {r_1}h) = \dfrac{{{\lambda _1}h}}{{{\varepsilon _0}}}$
$\therefore E = \dfrac{{{\lambda _1}}}{{2\pi {\varepsilon _0}{r_1}}}$

(ii) Similarly for second part consider a Gaussian cylinder of radius ${r_2}$ of outside cylinder

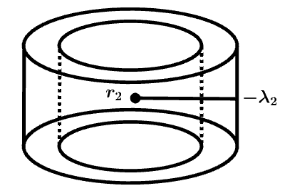
So net charge enclosed within Gaussian cylinder is $q = ({\lambda _1} - {\lambda _2})h$
And Flux enclosed is $\phi = E\int {ds = E(2\pi {r_2}h)}$ as $\int {ds = 2\pi {r_2}h}$
So from gauss law $\phi = \dfrac{q}{{{\varepsilon _0}}}$
Putting values we get,
$E(2\pi {r_2}h) = \dfrac{{({\lambda _1} - {\lambda _2})h}}{{{\varepsilon _0}}}$
$\therefore E = \dfrac{{({\lambda _1} - {\lambda _2})}}{{2\pi {\varepsilon _0}{r_2}}}$

Note: It should be remembered that area of curved part is only considered because area vector of disc part is perpendicular to field so it makes no contribution in flux also charges are distributed uniformly only on length of cylinder. From calculation it is clear that the electric field is not continuous everywhere in space around the cylinder.