Question
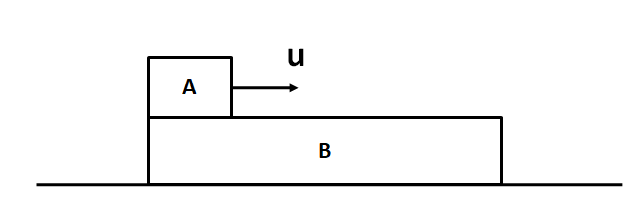
Question: A long block B rests on a smooth horizontal plane. A small block A of mass half that of B is placed ...
A long block B rests on a smooth horizontal plane. A small block A of mass half that of B is placed at one end of B and given a horizontal velocity, u . If μ is the coefficient of friction between the two block, then the time elapsed before the two block attain a common velocity is nμg2u , where n is
Solution
To solve this question, we have to determine the common velocity of the two blocks using the conservation of momentum. Then, using the kinematic equation of motion, we can find out the required time.
Formula Used:
⇒v=u+at , here v is the final velocity, u is the initial velocity, a is the acceleration, and t is the time.
⇒f=μN , here f is the limiting value of friction, μ is the coefficient of friction, and N is the normal reaction.
Complete step by step solution:
Let the mass of the long block be M and that of the small block be m
Also, let the common velocity attained by the two blocks be v .
Now, the horizontal plane below block B is smooth. So, there is no frictional force on the block B. The only frictional force present is in between the two blocks. Hence, there is no external force on the two blocks. Therefore, the total momentum of the two blocks is conserved. This means
Total initial momentum = Total final momentum
⇒mu+M(0)=(m+M)v
⇒(m+M)v=mu
So we get the common velocity as
⇒v=m+Mmu ………………...(i)
Now, considering the free body diagram of the block A
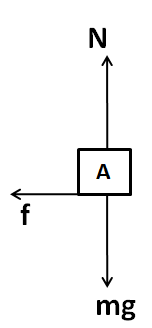
As there is no vertical motion of the block, so we can write
⇒N=mg …………………….(ii)
Here f is the frictional force on the block. Since there is relative motion in between the blocks A and B, so maximum limiting value of the friction must be present in between. We know that this value is given by
⇒f=μN
From (ii)
⇒f=μmg
So, this is the force acting on the block A. Since this force is opposite to its velocity, we place a negative sign so that
⇒f=−μmg
Now, the acceleration of the block is
⇒a=mf
⇒a=m−μmg=−μg …………………….(iii)
Now, from the first equation of motion, we have
⇒v=u+at
From (i) and (iii)
⇒m+Mmu=u−(μg)t
⇒(μg)t=u−m+Mmu
Taking u common, we have
⇒(μg)t=u(1−m+Mm)
⇒(μg)t=m+MMu
So, we get the time as
⇒t=μg(m+M)Mu …………………...(iv)
According to the question, we have
⇒m=2M
Or M=2m ………………….(v)
Substituting (v) in (iv)
⇒t=μg(m+2m)2mu
⇒t=μg(3m)2mu
Cancelling m , we finally get
⇒t=3μg2u ……………..(vi)
According to the question, we have
⇒t=nμg2u …………………...(vii)
Equating (vi) and (vii), we get
⇒n=3
Hence the value of n is 3.
Note:
We can also consider the frictional force on the long block B, from which its acceleration can be calculated. Then, using the same kinematic equation of motion with the initial velocity as zero, we can find out the time required.
