Question

$\log_3(\log_9x + \frac{1}{2} + 9^x) = 2x$

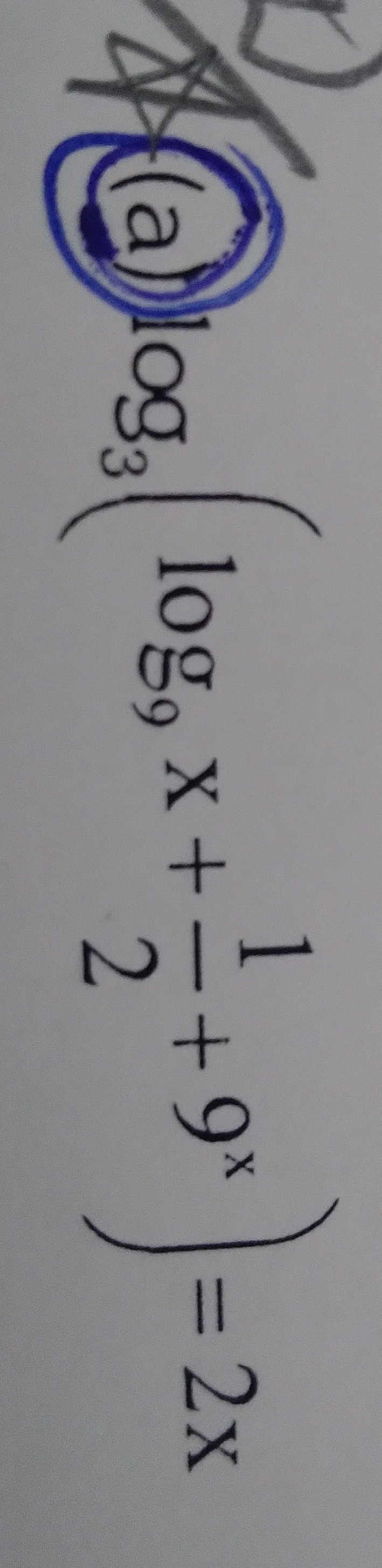
Answer 1

$\frac{1}{3}$

Answer 2

The given equation is: $\log_3\left(\log_9x + \frac{1}{2} + 9^x\right) = 2x$ Rewrite the right side of the equation using the property $a = \log_b(b^a)$: $2x = \log_3(3^{2x}) = \log_3((3^2)^x) = \log_3(9^x)$ The equation becomes: $\log_3\left(\log_9x + \frac{1}{2} + 9^x\right) = \log_3(9^x)$ For the logarithms to be equal, their arguments must be equal, provided the arguments are positive: $\log_9x + \frac{1}{2} + 9^x = 9^x$ Subtract $9^x$ from both sides: $\log_9x + \frac{1}{2} = 0$ $\log_9x = -\frac{1}{2}$ Convert this logarithmic equation to an exponential equation using the definition $\log_b y = z \iff y = b^z$: $x = 9^{-\frac{1}{2}}$ Calculate the value of $x$: $x = \frac{1}{9^{\frac{1}{2}}} = \frac{1}{\sqrt{9}} = \frac{1}{3}$ Verify the solution by checking the domain conditions:

1. For $\log_9x$ to be defined, $x > 0$. Our solution $x = \frac{1}{3}$ satisfies this ($\frac{1}{3} > 0$).
2. For the outer logarithm $\log_3(\dots)$ to be defined, its argument must be positive: $\log_9x + \frac{1}{2} + 9^x > 0$. Substitute $x = \frac{1}{3}$: $\log_9\left(\frac{1}{3}\right) + \frac{1}{2} + 9^{\frac{1}{3}}$ We know that $\log_9\left(\frac{1}{3}\right) = \log_{3^2}(3^{-1}) = \frac{-1}{2}\log_3 3 = -\frac{1}{2}$. So, the expression becomes: $-\frac{1}{2} + \frac{1}{2} + 9^{\frac{1}{3}} = 0 + \sqrt[3]{9} = \sqrt[3]{9}$ Since $\sqrt[3]{9} > 0$, the argument is positive, and the solution $x = \frac{1}{3}$ is valid. Check the original equation with $x = \frac{1}{3}$: Left Hand Side (LHS): $\log_3\left(\log_9\left(\frac{1}{3}\right) + \frac{1}{2} + 9^{\frac{1}{3}}\right) = \log_3\left(-\frac{1}{2} + \frac{1}{2} + \sqrt[3]{9}\right) = \log_3(\sqrt[3]{9}) = \log_3(9^{\frac{1}{3}}) = \frac{1}{3}\log_3 9 = \frac{1}{3} \times 2 = \frac{2}{3}$ Right Hand Side (RHS): $2x = 2 \times \frac{1}{3} = \frac{2}{3}$ Since LHS = RHS, the solution $x = \frac{1}{3}$ is correct.