Solveeit Logo
Login

Question

Question: A log of wood of length \(l\) and mass \(M\) is floating on the surface of a river perpendicular to ...

A log of wood of length ll and mass MM is floating on the surface of a river perpendicular to the banks. One end of the log touches the banks. A man of mass mm
standing at the other end walks towards the bank. Calculate the displacement of the log when he reaches the nearer end of the log.

Explanation

Solution

Here we have to first find the initial displacement and then the final displacement and then equate them to get the final answer.

Complete step by step solution:
Given,
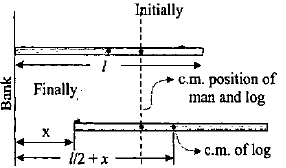
A log of wood of length ll and mass MM is floating on the surface of a river perpendicular to the banks. One end of the log touches the banks. A man of mass mm standing at the other end walks towards the bank.

We know that,
If a system does not undergo any external force, the system’s centre of mass will remain at rest or if it is travelling, will travel at a constant velocity.
Basically, due to Newton’s laws, the centre of mass of a body can be viewed as a point mass.
Let RORO be the wooden log. Since, there is no outside force; man’s centre of mass and the log system remain at rest. Let origin PP be the bank of the river. The guy is at point OO originally.
According to question,
m=m = mass of man
M=M = mass of log
x=x = displacement of log with respect to water
The initial displacement is:
xinitial=ml+M(l2)m+M{x_{initial}} = \dfrac{{ml + M\left( {\dfrac{l} {2}} \right)}} {{m + M}}

The final displacement is:
xinitial=ml+M(l2+x)m+M{x_{initial}} = \dfrac{{ml + M\left( {\dfrac{l} {2} + x} \right)}} {{m + M}}

Now let us equate the two displacements:
xinitial=xfinal ml+Ml2=mx+Ml2+Mx x=mlm+M  {x_{initial}} = {x_{final}} \\\ ml + \dfrac{{Ml}} {2} = mx + \dfrac{{Ml}} {2} + Mx \\\ x = \dfrac{{ml}} {{m + M}} \\\

Hence, the displacement of the log when he reaches the nearer end of the log is
x=mlm+Mx = \dfrac{{ml}}{{m + M}}

Additional information:
If no external force operates on the system, the system’s net linear momentum is conserved. If any external force operates on the system, the system’s portion of momentum, along which no external force is present or their vector sum is zero, is conserved.

Note:
Here we have to be careful while calculating the initial and final displacements. If we write the exchange values then, the answer would be wrong.