Question

A local train leaves station A; it gains speed at the rate of $1m{{s}^{-2}}$ for first $6s$ and then at the rate of $1.5m{{s}^{-2}}$ until it reached the speed of $12m{{s}^{-1}}$. The train maintains the same speed until it approaches station B; brakes are then applied, giving the train a constant deceleration and bringing it to a stop in $6s$. If the total running time of the train is $40s$. Find-
(a). distance between stations A and B
(b). Draw acceleration-time, velocity-time and position-time relation of motion.

Answer 1

A train is in different states at different intervals of time. For the first six seconds it acts under acceleration, since acceleration is constant, we can use the equation of motion to calculate distance and time for the second state. After the train starts moving with uniform velocity, its distance can be calculated using the formula of velocity. Applying the condition of deceleration, we can again use the equation of motion to calculate distance. Add the distance travelled by the train in different states to calculate total distance travelled.
Formulas used:
$v=u+at$
${{v}^{2}}={{u}^{2}}+2as$
$v=\dfrac{d}{t}$

Complete answer:
Given, after leaving station A, train accelerates at $1m{{s}^{-2}}$ for $6s$, $u=0$
We know that, according to equation of motion,
$v=u+at$
Here, $v$ is the final velocity
$u$ is the initial velocity
$a$ is the acceleration
$t$ is the time taken
In the above equation, substituting given values we get,
$\begin{aligned} & v=0+1\times 6 \\\ & \Rightarrow v=6m{{s}^{-1}} \\\ \end{aligned}$
It accelerates uniformly until it attains a speed of $6m{{s}^{-1}}$
Distance covered in this time is given by the equation of motion,
${{v}^{2}}={{u}^{2}}+2as$ - (1)
Here, $s$ is the distance travelled by the train in given time
In the above equation, substituting given values to get,
$\begin{aligned} & {{(6)}^{2}}=0+2\times 1\times s \\\ & \Rightarrow 36=2s \\\ & \therefore s=18m \\\ \end{aligned}$
Therefore, the distance that the train travels is $18m$.
After $6s$, the train accelerates at $1.5m{{s}^{-2}}$, $v=12m{{s}^{-1}}$, $u=6m{{s}^{-1}}$
In eq (1), we substitute given values to get,
$\begin{aligned} & {{(12)}^{2}}={{(6)}^{2}}+2\times 1.5\times s \\\ & \Rightarrow 144-36=3s \\\ & \Rightarrow \dfrac{108}{3}=s \\\ & \therefore s=36m \\\ \end{aligned}$
Therefore, the distance that the train travels in this time interval is $36m$.
Time taken can be calculated using the equation of motion
$v=u+at$
In the above equation, substituting given values we get,
$\begin{aligned} & 12=6+1.5\times t \\\ & \Rightarrow 1.5t=6 \\\ & \therefore t=4s \\\ \end{aligned}$
Therefore, the time taken by the train is $4s$.
Now, the train is decelerating uniformly, given,
$u=12m{{s}^{-1}}$, $v=0$, $t=6s$
Using the equation of motion,
$v=u+at$
In the above equation, substituting given values we get,
$\begin{aligned} & 0=12-a\times 6 \\\ & \Rightarrow 6a=12 \\\ & \therefore a=2m{{s}^{-2}} \\\ \end{aligned}$
The train is decelerating at $2m{{s}^{-2}}$. Using eq (1), we calculate the distance travelled, therefore, substituting given values in eq (1),
$\begin{aligned} & 0={{(12)}^{2}}-2\times 2\times s \\\ & \Rightarrow 4s=144 \\\ & \therefore s=36m \\\ \end{aligned}$
The time taken by the train to travel from station A to station B is
$40-(6+6+4)=24s$
For the interval of $24s$ the train travels with a uniform velocity of $12m{{s}^{-1}}$ therefore,
$\begin{aligned} & v=\dfrac{d}{t} \\\ & \Rightarrow vt=d \\\ \end{aligned}$
In the above equation, substituting given values to get,
$\begin{aligned} & 12\times 24=d \\\ & \Rightarrow d=288m \\\ \end{aligned}$
Therefore, the distance travelled in this interval is $288m$.
The total distance that the train travels is
$288+18+36+36=378m$
Therefore, the total distance that the train travels is $378m$.
The acceleration-time graph is-

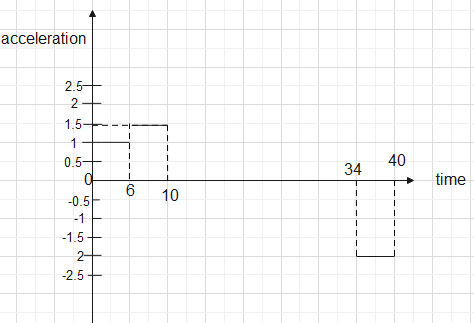
The velocity time graph is-

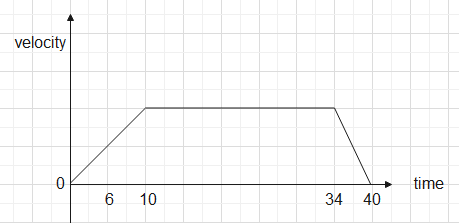
The position-time graph is-

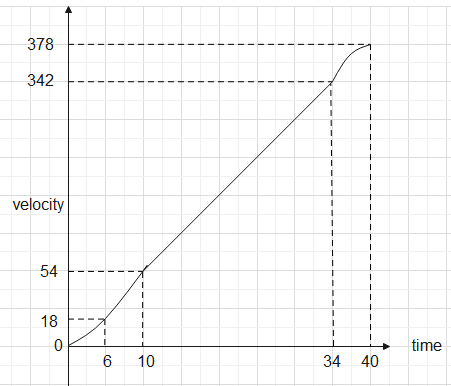
Therefore, the total distance that the train travels is $378m$. The velocity-time, acceleration-time and position-time graphs depict different relations.

Note:
When the force acting on a body is constant, its acceleration is also constant. Equations of motion are used when the acceleration of a body is constant. When a body is moving in uniform motion or with constant velocity, according to the second law of motion, no external force acts on it.