Question

A loaded spring gun of mass $M$ fires a shot of mass $m$with a velocity $v$ at an angle of elevation $\theta$. The gun was initially at rest on a horizontal surface. After firing, the centre of mass of the gun-shot system:
A) moves with velocity $\dfrac{{mv}}{M}$ .
B) moves with velocity $\dfrac{{mv}}{{M\cos \theta }}$ in the horizontal direction.
C) remains at rest.
D) moves with velocity $\dfrac{{\left( {M - m} \right)v}}{{\left( {M + m} \right)}}$ in the horizontal direction.

Answer 1

Here, when the shot is fired by the gun, the gun recoils backwards along the horizontal direction. This is a reaction to the action of firing the gun. The linear momentum of the gun-shot system is conserved throughout the firing since no external forces come into play.

Formula used:
-The linear momentum of a two-body system is given by, $p = Mv' + mv$ where $M$ and $m$ are the masses of the two bodies while $v'$ and $v$ are the respective velocities of the bodies.

Complete step by step answer.
Step 1: Sketch an appropriate diagram describing the gun-shot system and list the key parameters involved.

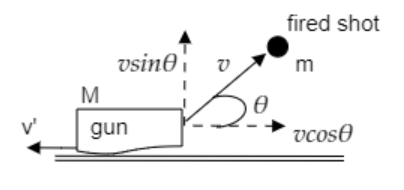
The above figure describes the gun-shot system under consideration.
The mass of the gun and that of the shot are denoted by $M$ and $m$ respectively.
The shot can be observed to move with the velocity $v$ making an angle $\theta$ with the horizontal direction. So, its horizontal component is $v\cos \theta$ and its vertical component is $v\sin \theta$.
Let $v'$ be the recoiling velocity of the gun.
Step 2: Using the conservation of the linear momentum, express the linear momentum of the system in the horizontal direction.
The conservation of momentum requires the linear momentum of the gun-shot system to remain constant before and after the firing in the horizontal direction.
The linear momentum of the system before firing is zero since the system is initially at rest. After firing, the velocities of the gun and the shot are $- v'$ and $v\cos \theta$ respectively in the horizontal direction.
Thus, in the horizontal direction, the linear momentum conservation gives us $- Mv' + mv\cos \theta = 0$
This implies that the net momentum of the system is zero along the horizontal direction.
Step 3: Based on the theory of conservation of linear momentum, we can deduct if the centre of mass of the system moves or not.
In the horizontal direction, the linear momentum is conserved i.e., no external force acts. Also initially, the system is said to be stationary. The centre of mass of the gun-shot system moves in the horizontal direction only if an external force acts on the system in that direction. Since no such forces are present, the centre of mass will not move along the horizontal direction.

So, the correct option must be C.

Note: The centre of mass of the gun-shot system may have a movement in the vertical direction. This is because the bullet may move vertically upwards but the gun cannot move vertically downwards as it is placed on a horizontal surface i.e., the recoil velocity of the gun has no vertical component.