Question

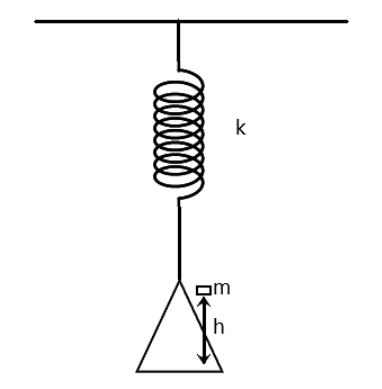
A load of mass $m$ falls from a height $h$ on a scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass does not bounce relative to the pan, then the amplitude of vibration is:

Answer 1

At the farthest point of extension, the change in gravitational potential energy of the load must be equal to the elastic potential energy of the spring. The amplitude is the maximum initial extension minus the equilibrium position if the mass had been placed carefully on the pan
Formula used: In this solution we will be using the following formulae;
${E_s} = \dfrac{1}{2}k{x^2}$ where ${E_s}$ is the energy stored in a spring, $k$ is the spring constant, and $x$ is the extension of the spring from initial position.
${E_p} = mgd$where${E_p}$ is the gravitational potential energy, $m$ is the mass of the body $g$ is acceleration due to gravity and $d$ is displacement from a reference point.
$x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$where$x$ is the root (solution) of a quadratic equation given as $a{x^2} + bx + c = 0$.

Complete Step-by-Step solution:
Choosing the point of reference to be at the point of drop. Then the energy conservation at the farthest point of extension of the spring would be written as
$mgh + mgx = \dfrac{1}{2}k{x^2}$ where $m$ is the mass, $g$ is acceleration due to gravity, $h$ is the height of mass from pan, $x$ is the initial extension of the string from original position and $k$ is the spring constant of the spring.
Hence, by multiplying through by 2 and dividing through by $k$, then rearranging, we have
${x^2} - \dfrac{{2mg}}{k}x - \dfrac{{2mgh}}{k} = 0$
We see that, this is a quadratic equation. Hence using the quadratic formula given by
$x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$for a quadratic equation $a{x^2} + bx + c = 0$
Hence,
$x = \dfrac{{ - \left( { - \dfrac{{2mg}}{k}} \right) \pm \sqrt {{{\left( { - \dfrac{{2mg}}{k}} \right)}^2} - 4\left( 1 \right)\left( { - \dfrac{{2mgh}}{k}} \right)} }}{{2\left( 1 \right)}}$
$\Rightarrow x = \dfrac{{mg}}{k} \pm \dfrac{1}{2}\sqrt {4{{\left( {\dfrac{{mg}}{k}} \right)}^2} + 4\left( {\dfrac{{2mgh}}{k}} \right)}$
We can factorise $4{\left( {\dfrac{{mg}}{k}} \right)^2}$within the root, so we have
$x = \dfrac{{mg}}{k} \pm \dfrac{1}{2}\sqrt {4{{\left( {\dfrac{{mg}}{k}} \right)}^2}\left( {1 + \dfrac{{2mgh}}{k}} \right)}$
$\Rightarrow x = \dfrac{{mg}}{k} \pm \left( {\dfrac{{mg}}{k}} \right)\sqrt {1 + \dfrac{{2mgh}}{k}}$
Now, we see that the term after the $\pm$ is larger than the term before it. Hence, we can neglect the negative as in
$x = \dfrac{{mg}}{k} + \left( {\dfrac{{mg}}{k}} \right)\sqrt {1 + \dfrac{{2mgh}}{k}}$
Now, amplitude would be equal to
$A = x - {x_0}$where${x_0}$ would be the equilibrium position.
The equilibrium position will be the point where the weight balances the spring force. i.e.
$mg = k{x_0}$
$\Rightarrow {x_0} = \dfrac{{mg}}{k}$
Hence, by subtracting from $x$, we have
$x = \dfrac{{mg}}{k} + \dfrac{{mg}}{k}\sqrt {1 + \dfrac{{2mgh}}{k}} - \dfrac{{mg}}{k}$
$\Rightarrow x = \dfrac{{mg}}{k}\sqrt {1 + \dfrac{{2mgh}}{k}}$

Note: for clarity, the conservation of energy equation can be given as $mgh + mgx = \dfrac{1}{2}k{x^2}$ for the following reason. Assuming the potential is zero at height $h$ but increasing downward. The total energy at that point is hence,
${E_s} + {E_p} + {E_k} = 0$where${E_k}$ is kinetic energy. Now, at the point where the mass just hit the pan, the mass gains energy is${E_s} + {E_p} + {E_k} = - mgh + \dfrac{1}{2}m{v^2}$ (only potential and kinetic energy exist). At the point of maximum extension the total energy becomes ${E_s} + {E_p} + {E_k} = - mgh - mgx + \dfrac{1}{2}k{x^2}$ since kinetic energy would be zero. From conservation of energy, total energy is constant, hence
${E_s} + {E_p} + {E_k} = - mgh - mgx + \dfrac{1}{2}k{x^2} = 0$
$\Rightarrow mgh + mgx = \dfrac{1}{2}k{x^2}$
note that the reference point of the potential energy is strictly for convenience, and it can be chosen from any point. But one must observe the convention that objects higher than the reference point have positive gravitational potential energy and objects lower than the reference point have negative potential energy.