Question

A load of mass $1{\text{kg}}$ is attached to one end of a steel wire of cross-sectional area $3{\text{m}}{{\text{m}}^2}$ and Young’s modulus ${\text{1}}{{\text{0}}^{11}}{\text{N}}{{\text{m}}^{ - 2}}$. The other end is suspended vertically from a hook on a wall. The load is then pulled horizontally and released. Find the fractional change in length as the load passes through its lowest position. (Given $g = 10{\text{m}}{{\text{s}}^{ - 1}}$ ).
A) ${\text{0}}{\text{.3}} \times {\text{1}}{{\text{0}}^{ - 4}}$
B) ${\text{0}}{\text{.3}} \times {\text{1}}{{\text{0}}^{ - 3}}$
C) ${\text{1}}{{\text{0}}^3}$
D) ${\text{1}}{{\text{0}}^4}$

Answer 1

At the lowest position the force on the load will be the force of gravity. Young’s modulus of a material refers to the stiffness of a material. It depends on the mass of the load, the area of the wire and the fractional change in length of the wire.

Formula used:
-The Young’s modulus of a material is given by, $Y = \dfrac{{\left( {\dfrac{F}{A}} \right)}}{{\left( {\dfrac{{\Delta l}}{l}} \right)}}$ where $F$ is the force acting on the load, $A$ is the area of cross-section of the wire and $\dfrac{{\Delta l}}{l}$ is the fractional change in length.

Complete step by step answer.
Step 1: Sketch a figure of the arrangement mentioned in the question and list the parameters known.

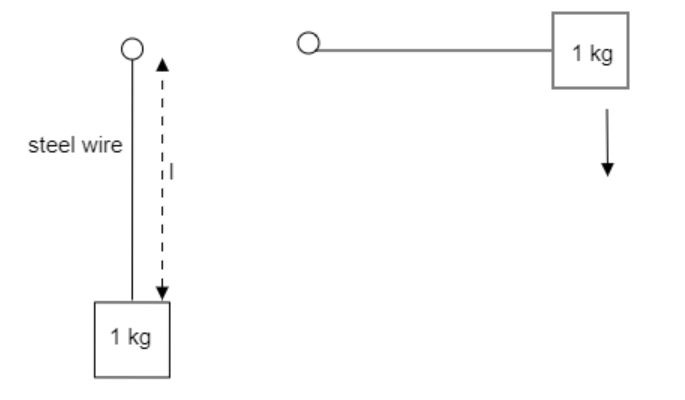
The mass of the load is given to be $m = 1{\text{kg}}$ .
The Young’s modulus of the steel wire is $Y = {\text{1}}{{\text{0}}^{11}}{\text{N}}{{\text{m}}^{ - 2}}$ and its area of cross-section is $A = 2{\text{m}}{{\text{m}}^2}$ .
Step 2: Express the relation for Young's modulus of the steel wire to find the fractional change in length.
The Young’s modulus of a material is given by, $Y = \dfrac{{\left( {\dfrac{F}{A}} \right)}}{{\left( {\dfrac{{\Delta l}}{l}} \right)}}$ ---------- (1)
where $F$ is the force acting on the load, $A$ is the area of cross-section of the wire and $\dfrac{{\Delta l}}{l}$ is the fractional change in length.
At the lowest position, the load will be vertically downwards and the force acting on the load will be the force of gravity given by, $F = mg$ .
Equation (1) can be rearranged to obtain an expression for the fractional change in length of the steel wire i.e., $\left( {\dfrac{{\Delta l}}{l}} \right) = \dfrac{F}{{AY}}$ or, $\left( {\dfrac{{\Delta l}}{l}} \right) = \dfrac{{mg}}{{AY}}$ -------- (2)
Substituting the values for $m = 1{\text{kg}}$, $Y = {\text{1}}{{\text{0}}^{11}}{\text{N}}{{\text{m}}^{ - 2}}$, $A = 2{\text{m}}{{\text{m}}^2}$ and $g = 10{\text{m}}{{\text{s}}^{ - 1}}$ in equation (2) we get, $\left( {\dfrac{{\Delta l}}{l}} \right) = \dfrac{{1 \times 10}}{{3 \times {{10}^{ - 6}} \times {{10}^{11}}}} = 0.3 \times {10^{ - 4}}$
Thus the fractional change in length is $\left( {\dfrac{{\Delta l}}{l}} \right) = 0.3 \times {10^{ - 4}}$ .

Hence the correct option is A.

Note: The fractional change in length of the wire essentially suggests how much the wire stretches relative to its original length when the load of 1 kg was placed at its one end. While substituting values in an equation make sure that all the values are expressed in their respective S.I. units. If not, the necessary conversion of units must be done. Here, the area expressed in mm2 is converted to m2 during substitution.