Question

A load is placed in an elevator to give a combined mass of $1800{\text{kg}}$. Find the tension in the elevator cables when it moves down with a retardation of $2{\text{m/}}{{\text{s}}^2}$. (Take $g = 10{\text{m/}}{{\text{s}}^2}$ ).
a. 14400 N
b. 21600 N
c. 1800 N
d. 20000 N

Answer 1

The combined system of the elevator with its load has two forces acting on it. One is the combined force of gravity acting downward and the tension on the supporting cables acting upward.

Complete step by step answer:
Step 1:
Sketch a free body diagram of the problem at hand.

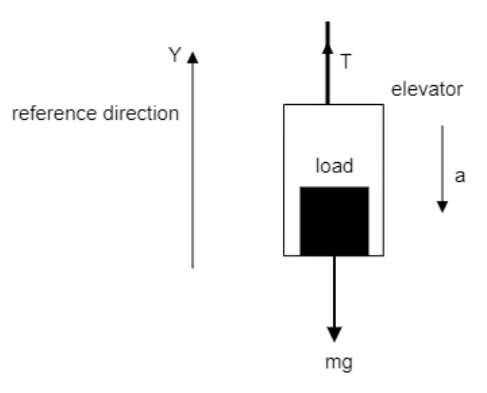
Step 2:
List the data given in the question.
The combined mass of the elevator and load is $m = 1800{\text{kg}}$ . The elevator- load setup forms the system that is under consideration.
The elevator moves down with retardation of $2{\text{m/}}{{\text{s}}^2}$ .
The positive Y direction is taken as the reference direction for the motion of the elevator. So, the retardation is $a = - 2{\text{m/}}{{\text{s}}^2}$ .

Step 3:
Obtain an expression for the net force acting on the system.
The combined force of gravity of the system is $W = mg$ and it is directed downwards.
The tension in the cables is $T$ and it is directed upwards.
Newton’s second law of motion provides a relation for the force acting on a body of mass $m$moving with an acceleration $a$, i.e., $F = ma$ .
Then net force acting on the system is given by,
$F = ma = T - W$ .

Step 4:
Obtain a relation for tension $T$ from the net force equation.
Substituting for $W$ in (1) we get, $ma = T - mg$ ------ (1).
Rearrange equation (1) to obtain a relation for tension $T$ .
Then we have, $T = m(a + g)$ .

Step 5:
Find the tension in the supporting cables by substituting the known quantities.
The relation for tension is $T = m(a + g)$ .
Substituting the values for, $m = 1800{\text{kg}}$ , $a = - 2{\text{m/}}{{\text{s}}^2}$ and $g = 10{\text{m/}}{{\text{s}}^2}$ in the above equation, we get $T = 1800( - 2 + 10) = 14400{\text{N}}$ .
Therefore, the tension in the elevator cables is $T = 14400{\text{N}}$ .

Hence, the correct answer is option (A).

Note: The reference direction for the motion of the system is arbitrary. If the negative Y direction was considered as the reference direction, then the retardation will be expressed as a positive quantity, i.e., $a = 2{\text{m/}}{{\text{s}}^2}$ . The tension in the supporting cables remains the same.