Solveeit Logo
Login

Question

Question: A liquid rises to a height of 7 cm in a capillary tube of radius 0.1mm. The density of the liquid is...

A liquid rises to a height of 7 cm in a capillary tube of radius 0.1mm. The density of the liquid is 0.8×103kgm−30.8\times {{10}^{3}}kg{{m}^{-3}}. If the angle of contact between the liquid and the surface of the tube is zero, calculate the surface tension. Take g = 10ms−2m{{s}^{-2}}.
A. 3.8×10−2Nm−1\text{A}\text{. }3.8\times {{10}^{-2}}N{{m}^{-1}}
B. 2.2×10−2Nm−1\text{B}\text{. 2}.2\times {{10}^{-2}}N{{m}^{-1}}
C. 2.8×10−2Nm−1\text{C}\text{. 2}.8\times {{10}^{-2}}N{{m}^{-1}}
D. 2.8×10−4Nm−1\text{D}\text{. 2}.8\times {{10}^{-4}}N{{m}^{-1}}

Explanation

Solution

The height of the liquid to which it rises inside a capillary tube is given as h=2Tcos⁡θrρgh=\dfrac{2T\cos \theta }{r\rho g}. Substitute the given values in this formula and find the value of the surface tension of the liquid (T).
Formula used:
h=2Tcos⁡θrρgh=\dfrac{2T\cos \theta }{r\rho g}

Complete answer:
When a capillary tube is partially dipped vertically into a liquid, the liquid enters the capillary tube and rises higher than the level of the liquid outside the capillary.
The height to which the liquid rises inside the capillary is given as h=2Tcos⁡θrρgh=\dfrac{2T\cos \theta }{r\rho g} …. (i).
Here, h is the height of the liquid in the capillary,
T is the surface tension of the liquid,
θ\theta is the angle of contact between surface of the capillary and the liquid,
r is the radius of the capillary,
ρ\rho is the density of the liquid and g is acceleration due to gravity.

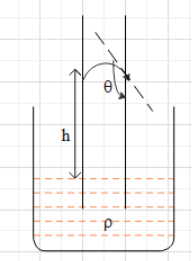
In the question, it is given that the liquid rises to a height of 7cm in the capillary. Hence, h = 7cm = 0.07m.
The angle of contact between the liquid and the surface of the tube is said to be zero. Hence, θ=0\theta =0.
The radius of the tube is 0.1mm. Hence, r=0.1mm=0.1×10−3mr=0.1mm=0.1\times {{10}^{-3}}m .
The density of the given liquid is ρ=0.8×103kgm−3\rho =0.8\times {{10}^{3}}kg{{m}^{-3}}.
It is given that g = 10ms−2m{{s}^{-2}}.
Substitute the values in equation (i).
⇒0.07m=2Tcos⁡0(0.1×10−3)(0.8×103kgm−3)(10)\Rightarrow 0.07m=\dfrac{2T\cos 0}{\left( 0.1\times {{10}^{-3}} \right)\left( 0.8\times {{10}^{3}}kg{{m}^{-3}} \right)(10)}.
We know that cos⁡0\cos 0= 1.
⇒0.07m=2T(0.1×10−3)(0.8×103kgm−3)(10)\Rightarrow 0.07m=\dfrac{2T}{\left( 0.1\times {{10}^{-3}} \right)\left( 0.8\times {{10}^{3}}kg{{m}^{-3}} \right)(10)}
⇒T=0.07(0.1×10−3)(0.8×103kgm−3)(10)2=0.028=2.8×10−2Nm−1\Rightarrow T=\dfrac{0.07\left( 0.1\times {{10}^{-3}} \right)\left( 0.8\times {{10}^{3}}kg{{m}^{-3}} \right)(10)}{2}=0.028=2.8\times {{10}^{-2}}N{{m}^{-1}}.
Therefore, the surface of the given liquid is 2.8×10−2Nm−12.8\times {{10}^{-2}}N{{m}^{-1}}.

Hence, the correct option is C.

Note:
Do not confuse between tension and surface tension.
Tension is the internal force produced inside in a string or a wire when it is stretched by applying a force.
Surface tension is the force exerted by the liquid per unit length on the surface of the liquid.
Hence, both tension and surface tension tell us about force but they are not the same quantities.