Question

A liquid of density $\rho$ is filled in a U-tube, whose one end is open & at the other end a bulb is fitted whose pressure is ${{P}_{A}}$. Now this tube is moved horizontally with acceleration 'a' as shown in the figure. During motion it is found that liquid in both columns is at the same level at equilibrium. If atmospheric pressure is ${{P}_{0}}$, then find the value of ${{P}_{A}}$

Answer 1

As the tube is accelerating so it constitutes a non-inertial frame of reference. For fluid problems we have to see the fluid in an inertial frame of reference. So first consider the observer to rest in the tube frame. i.e. a man sitting above the tube. As the tube is accelerating the man will see that liquid inside the tube will experience a pseudo force. Due to pseudo force the pseudo acceleration of the liquid will be opposite to that of the acceleration of the tube. It is known that the pressure increases in the direction of acceleration and decreases in the direction of acceleration. So first calculate the pressure where the air is touching the liquid, and calculate the pressure when we go down and then calculate the pressure when we go right. Finally calculate the pressure at the bulb which will give the value of ${{P}_{A}}$.

Formulas used:
The pressure exerted by a liquid of density $\rho$ at a height $h$ along the direction of acceleration is
$P=\rho ah$
If we move opposite to the acceleration then the pressure at height $h$ is
$P=-\rho ah$

Complete answer:
Given that the liquid is in the same level when the tube is moving with acceleration $a$ to the right. As the tube is accelerating so the liquid inside the tube will experience a pseudo force opposite to the direction of the tube.
So the pseudo acceleration will be opposite to that of the tube acceleration. So the pseudo acceleration of the liquid will have magnitude same as the tube acceleration but opposite in direction. I.e. the direction of pseudo acceleration of the liquid is to the left.

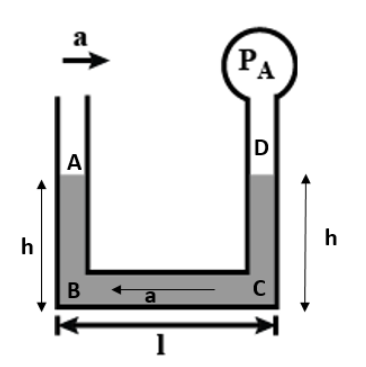
At point A the pressure will be only due to the atmospheric pressure. So at point A the pressure is
${{P}_{a}}={{P}_{0}}$.
When we move from point A to point B we move along the acceleration due to gravity and the vertical component of pseudo acceleration is zero so the pressure at point B which is at a height $h$ below A level is ${{P}_{b}}={{P}_{a}}+\rho gh={{P}_{0}}+\rho gh$.
When we move from point B to C we are moving against the pseudo acceleration covering a length $l$. The horizontal component of the acceleration due to gravity is zero. So the pressure will decrease because we are moving against the pseudo acceleration. So the pressure at point C is
${{P}_{c}}={{P}_{b}}-\rho al={{P}_{a}}+\rho gh-\rho al={{P}_{0}}+\rho gh-\rho al$
When we move from point C to D we are moving against the acceleration due to gravity covering a distance $h$. The vertical component of the pseudo acceleration is zero. So the pressure will decrease because we are moving against the acceleration due to gravity. So the pressure at point D which will be equal to the pressure at the bulb is
${{P}_{A}}={{P}_{d}}={{P}_{c}}-\rho gh={{P}_{0}}+\rho gh-\rho al-\rho gh={{P}_{0}}-\rho al$
So the pressure at the bulb is ${{P}_{A}}={{P}_{0}}-\rho al$

Note:
The liquid problems can only be solved in an inertial frame of reference. If the whole system is accelerating then we have to associate a frame of reference in which the liquid system is stationary or moving with constant velocity. Or you can assume the pseudo force to solve these types of problems.