Solveeit Logo
Login

Question

Question: A liquid in a beaker has temperature \[\theta \] at time t and \[{\theta _0}\] is the temperature of...

A liquid in a beaker has temperature θ\theta at time t and θ0{\theta _0} is the temperature of surroundings, then according to Newton’s law of cooling, correct graph between log⁡e(θ−θ0){\log _e}\left( {\theta - {\theta _0}} \right) and t is:
A.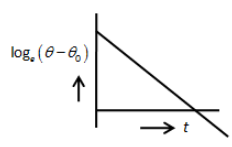
B.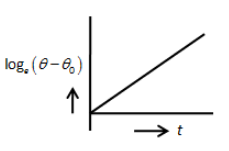
C.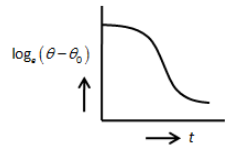
D.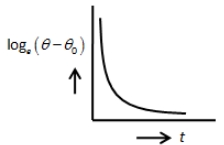

Explanation

Solution

According to Newton’s law of cooling the rate of heat loss with respect to time is proportional to the difference in the temperature of the body and temperature of the surrounding. Rearrange the expression for Newton’s law of cooling and rearrange it in the required form. Integrate it to get the relationship between log⁡e(θ−θ0){\log _e}\left( {\theta - {\theta _0}} \right) and time t.

Formula used:
Newton’s law of cooling, dθdt=−k(θ−θ0)\dfrac{{d\theta }}{{dt}} = - k\left( {\theta - {\theta _0}} \right)
Here, kk is the constant, θ\theta is the temperature of the body and θ0{\theta _0} is the temperature of the surrounding.

Complete step by step answer:
To understand the nature of the graph between log⁡e(θ−θ0){\log _e}\left( {\theta - {\theta _0}} \right) and t, we have to recall Newton’s law of cooling.According to Newton’s law of cooling the rate of heat loss with respect to time is proportional to the difference in the temperature of the body and temperature of the surrounding. Therefore, we can express Newton’s law of cooling as,
dθdt=−k(θ−θ0)\dfrac{{d\theta }}{{dt}} = - k\left( {\theta - {\theta _0}} \right)
Here, kk is the constant, θ\theta is the temperature of the body and θ0{\theta _0} is the temperature of the surrounding.

Let’s rearrange the above equation as follows,
dθθ−θ0=−kdt\dfrac{{d\theta }}{{\theta - {\theta _0}}} = - kdt
Integrating the above equation, we get,
∫dθθ−θ0=−k∫dt\int {\dfrac{{d\theta }}{{\theta - {\theta _0}}}} = - k\int {dt}
⇒∫dθθ−θ0=−kt+C\Rightarrow \int {\dfrac{{d\theta }}{{\theta - {\theta _0}}}} = - kt + C
We have, ∫1xdx=log⁡ex+C\int {\dfrac{1}{x}dx} = {\log _e}x + C.

Therefore, the above equation becomes,
log⁡e(θ−θ0)=−kt+C{\log _e}\left( {\theta - {\theta _0}} \right) = - kt + C
Thus, we can write,
log⁡e(θ−θ0)∝−t{\log _e}\left( {\theta - {\theta _0}} \right) \propto - t
Hence, the graph between log⁡e(θ−θ0){\log _e}\left( {\theta - {\theta _0}} \right) and t will be the straight-line but with negative slope.If we look at the given options, the option A is straight-line which has negative slope.

So, the correct answer is option A.

Note: While using Newton’s law of cooling formula, dθdt=−k(θ−θ0)\dfrac{{d\theta }}{{dt}} = - k\left( {\theta - {\theta _0}} \right), make sure that the heat loss is in the form of radiation only and no other source is used to decrease the temperature of the body. Also, the temperature of the surrounding must remain the same throughout the cooling process. The constant of integration C vanishes when you substitute the limits of integration.