Question

A line through origin meets the line $2x = 3y + 13$ at the right angle at point$Q$. Find the absolute difference of coordinates of$Q$.

Answer 1

In this problem, we need to find the slope of the line passing through the origin. Next, find the equation of the line passing through origin. Then, find the point of intersection of the two lines.

Complete step by step answer:

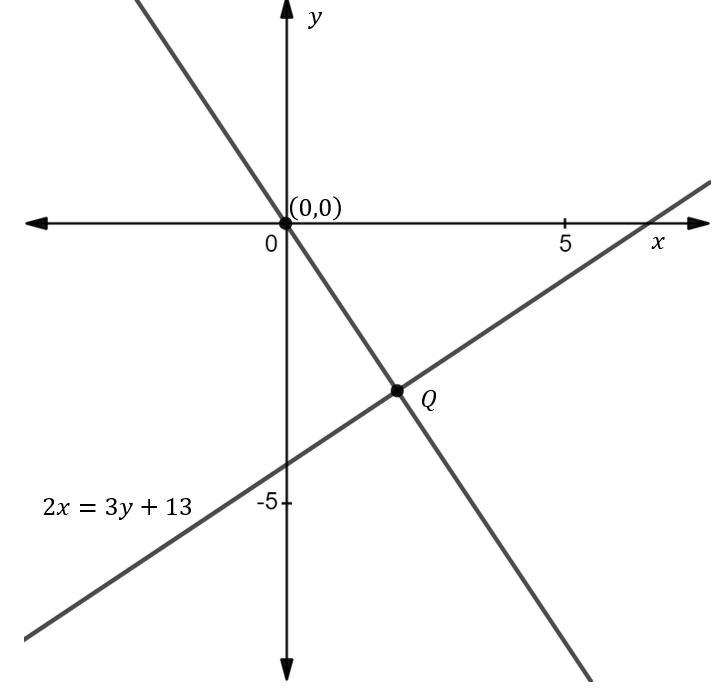
Rewrite, the given equation $\left( {2x = 3y + 13} \right)$ of the line ${L_1}$ in the form of $y = mx + c$ as shown below.

$$\,\,\,\,\,2x = 3y + 13 \\\ \Rightarrow 3y = 2x - 13 \\\ \Rightarrow y = \dfrac{2}{3}x - \dfrac{{13}}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,......\left( 1 \right) \\\$$

Compare, the above equation $y = \dfrac{2}{3}x - \dfrac{{13}}{3}$ with $y = mx + c$ to obtain the value of slope $m$.
$m = \dfrac{2}{3}$
Let, the slope of another line ${L_2} be {m_1}$.
As both the lines ${L_1}$ and ${L_2}$ intersect at right angle at point$Q$,

$$\,\,\,\,\,m \times {m_1} = - 1 \\\ \Rightarrow \dfrac{2}{3}{m_1} = - 1 \\\ \Rightarrow {m_1} = - \dfrac{3}{2} \\\$$

The equation of line passing through point $\left( {{x_1},{y_1}} \right)$ having slope ${m_1}$ is as follows:
$y - {y_1} = {m_1}\left( {x - {x_1}} \right)$
Since, the line ${L_2}$ passes through the origin $\left( {0,0} \right)$ and have slope $- \dfrac{3}{2}$, substitute 0 for ${x_1}$, 0 for ${y_1}$ and $- \dfrac{3}{2}$ for ${m_1}$ in above equation.

$$\,\,\,\,\,\,y - 0 = - \dfrac{3}{2}\left( {x - 0} \right) \\\ \Rightarrow y = - \dfrac{3}{2}x \\\ \Rightarrow 2y = - 3x \\\ \Rightarrow 2y + 3x = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,......\left( 2 \right) \\\$$

Now, the coordinate of the point $Q$ is obtained by solving the equation (1) and (2).
From, equation (1) substitute, $\dfrac{2}{3}x - \dfrac{{13}}{3}$ for $y$ in equation (2).

$$\,\,\,\,\,2\left( {\dfrac{2}{3}x - \dfrac{{13}}{3}} \right) + 3x = 0 \\\ \Rightarrow \dfrac{4}{3}x - \dfrac{{26}}{3} + 3x = 0 \\\ \Rightarrow 4x - 26 + 9x = 0 \\\ \Rightarrow 13x = 26 \\\ \Rightarrow x = 2 \\\$$

Substitute 2 for $x$ in equation (1) to obtain the value of$y$.

$$\,\,\,\,\,\,y = \dfrac{2}{3}\left( 2 \right) - \dfrac{{13}}{3} \\\ \Rightarrow y = \dfrac{{4 - 13}}{3} \\\ \Rightarrow y = \dfrac{{ - 9}}{3} \\\ y = - 3 \\\$$

Thus, the coordinate of the point $Q$ is $\left( {2, - 3} \right)$.

Note: When two lines intersect at right angles, the product of their slopes will be equal to -1. When two lines intersect each other, the intersection point is the solution of the two equations.