Question

A line segment has endpoints at $\left( {2,7} \right)$ and $\left( {5,4} \right)$. The line segment is dilated by a factor of $2$ around $\left( {4,3} \right)$. What are the new endpoints and length of the line segment?

Answer 1

Here, in the given question we are given, a line segment has endpoints at $\left( {2,7} \right)$ and $\left( {5,4} \right)$ and this line segment is dilated by a factor of $2$ around $\left( {4,3} \right)$ and we need to find the new points and length of the line segment. Dilation is a transformation, which is used to resize the object. Dilation is used to make the objects larger or smaller. At first we will find the new endpoints using the dilution factor. If a point $A$ of coordinate $\left( {a,b} \right)$ be dilated by a factor $n$ around the point of coordinate $\left( {h,k} \right)$, then after dilation the new position will be $A' = \left( {n\left( {a - h} \right) + h,n\left( {b - k} \right) + k} \right)$. After this, we will find the length of line segment of new end points using distance formula, $D = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$.

Complete step by step answer:
Let $\overline {PQ}$ be a line segment on the coordinate plane with endpoints at $\left( {2,7} \right)$ and $\left( {5,4} \right)$.
The absolute value of the scale factor $\left( n \right)$, with the constraint $0 < n < 1$, reduces the line segment $\overline {PQ}$, enlarges if otherwise.
The scale factor of dilation is $2$.
Now, let us find the new endpoints using $A' = \left( {n\left( {a - h} \right) + h,n\left( {b - k} \right) + k} \right)$
Given, endpoints $P\left( {2,7} \right)$ and $Q\left( {5,4} \right)$.
For point $P\left( {2,7} \right)$, we have $n = 2$ and $\left( {h,k} \right) = \left( {4,3} \right)$. So, new endpoint will be:
$\Rightarrow P' = \left( {2\left( {2 - 4} \right) + 4,2\left( {7 - 3} \right) + 3} \right)$
On subtraction of terms, we get
$\Rightarrow P' = \left( {2\left( { - 2} \right) + 4,2\left( 4 \right) + 3} \right)$
On multiplication of terms, we get
$\Rightarrow P' = \left( { - 4 + 4,8 + 3} \right)$
$\Rightarrow P' = \left( {0,11} \right)$
For point $Q\left( {5,4} \right)$, We have $n = 2$ and $\left( {h,k} \right) = \left( {4,3} \right)$. So, new endpoint will be:
$\Rightarrow Q' = \left( {2\left( {5 - 4} \right) + 4,2\left( {4 - 3} \right) + 3} \right)$
On subtraction of terms, we get
$\Rightarrow Q' = \left( {2\left( 1 \right) + 4,2\left( 1 \right) + 3} \right)$
On multiplication of terms, we get
$\Rightarrow Q' = \left( {2 + 4,2 + 3} \right)$
$\Rightarrow Q' = \left( {6,5} \right)$
New end-points: $P'\left( {0,11} \right)$ and $Q'\left( {6,5} \right)$.

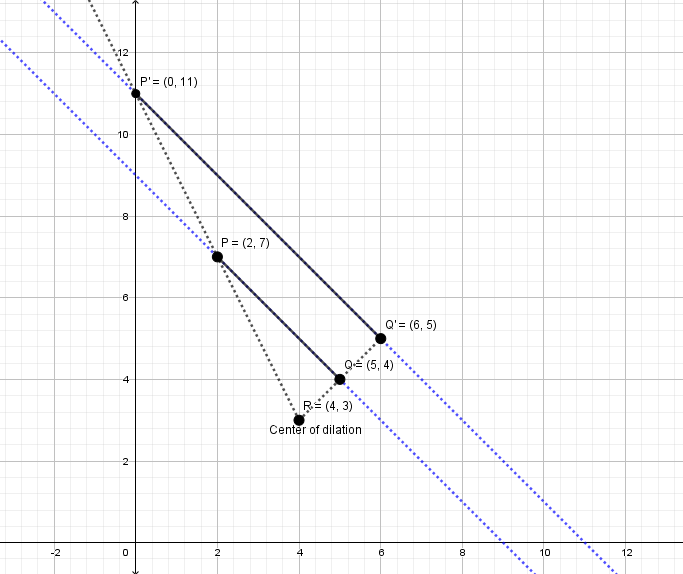
Here $\overline {PQ}$ is the pre-image and after dilation, $\overline {P'Q'}$ is called the image. Note that the pre-image and the image are parallel.
Observe that the points (center of dilation $R$, $P$ and $P'$) are collinear.
And, the points (center of dilation $R$, $Q$ and $Q'$) are collinear.
$\overline {PQ} \parallel \overline {P'Q'}$, since we have congruent corresponding angles.
Also, from $R\left( {4,3} \right)$, move up $4units$ on the $y - axis$, and $2units$ left on the $x - axis$ to reach the endpoint $P\left( {2,7} \right)$.
Move $\left( {4 \times 2 = 8units} \right)$ up on the $y - axis$, and $\left( {2 \times 2 = 4units} \right)$ left on the $x - axis$, to reach the point $P'\left( {0,11} \right)$.
From $R\left( {4,3} \right)$, move up $1unit$ on the $y - axis$, and $1unit$ right on the $x - axis$ to reach the endpoint $Q\left( {5,4} \right)$.
Move $\left( {1 \times 2 = 2units} \right)$ up on the $y - axis$, and $\left( {1 \times 2 = 2units} \right)$ to the right on the $x - axis$, to reach the point $Q'\left( {6,5} \right)$.
Now, we will find the length of the line segment or length of the image $\overline {P'Q'}$.
Distance formula: $D = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$, let $\left( {{x_1},{y_1}} \right)$ be $\left( {6,5} \right)$ and $\left( {{x_2},{y_2}} \right)$ be $\left( {0,11} \right)$. Therefore, on substituting the values, we get
$\Rightarrow D = \sqrt {{{\left( {0 - 6} \right)}^2} + {{\left( {11 - 5} \right)}^2}}$
On subtraction of terms, we get
$\Rightarrow D = \sqrt {{{\left( 6 \right)}^2} + {{\left( 6 \right)}^2}}$
$\Rightarrow D = \sqrt {36 + 36}$
On addition of terms, we get
$\Rightarrow D = \sqrt {72}$
$\Rightarrow D = 8.48$
Thus, length of line segment $\overline {P'Q'} = 8.48units$.
Therefore, the new endpoints are $P'\left( {0,11} \right)$ and $Q'\left( {6,5} \right)$ and length of line segment is $8.48units$.

Note: Remember that dilation is not an isometry. It creates similar figures only and dilation preserves the angle of measure. Remember that a scale factor of $n = 1$ means that the segment and its image are equal. The dilation does not enlarge or shrink the image of the figure; it remains unchanged. Also, when the scale factor $n > 1$, a dilation is an enlargement. When $0 < n < 1$, a dilation is a reduction.