Question

A line passing through the point with position vector $2\mathop i\limits^ \wedge - 3\mathop j\limits^ \wedge + 4\mathop k\limits^ \wedge$ and is perpendicular to the plane $\mathop r\limits^ \to .(3\mathop i\limits^ \wedge + 4\mathop j\limits^ \wedge - 5\mathop k\limits^ \wedge ) = 7$. Find the equation of the line in Cartesian and vector forms.

Answer 1

Vectors can be defined as a quantity possessing both direction and magnitude position vectors simply denote the position or location of a point in the three-dimensional Cartesian system with respect to a reference origin. Furthers, when the line is perpendicular to the plane the line will be parallel to the normal of the plane.

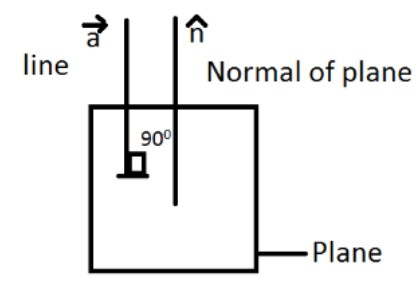
Equation of plane can be given a $\mathop r\limits^ \to .\mathop n\limits^ \to = d$ and the line having position vector $\mathop a\limits^ \to$and parallel to a given vector $\mathop b\limits^ \to$is given by $\mathop r\limits^ \to = \mathop a\limits^ \to + \lambda \mathop b\limits^ \to$.

Complete step by step solution:
Given position vector is $(\mathop a\limits^ \to ) = 2\mathop i\limits^ \wedge - 3\mathop j\limits^ \wedge + 4\mathop k\limits^ \wedge$
Now, given line which is perpendicular to plane will be parallel to the normal of the plane.
Finding normal of plane
$\mathop r\limits^ \to (3\mathop i\limits^ \wedge + 4\mathop j\limits^ \wedge - 5\mathop k\limits^ \wedge ) = 7$
As we know,
$E{q^n}$ of plane $\Rightarrow \mathop r\limits^ \to .\mathop n\limits^ \to = d$
We get $\mathop n\limits^ \to . = 3\mathop i\limits^ \wedge + 4\mathop j\limits^ \wedge - 5\mathop k\limits^ \wedge$
We known that parallel vectors are equal.
Let this vector be $\mathop b\limits^ \to = 3\mathop i\limits^ \wedge + 4\mathop j\limits^ \wedge - 5\mathop k\limits^ \wedge$
The vector equation of a line passing through a point with position vector $\mathop a\limits^ \to$ and parallel to $\mathop b\limits^ \to$ is.
$\mathop r\limits^ \to =$ position vector + $\lambda$ (parallel vector)
$\mathop r\limits^ \to = \mathop a\limits^ \to + \lambda \mathop b\limits^ \to$
$\Rightarrow \mathop r\limits^ \to = 2\mathop i\limits^ \wedge - 3\mathop i\limits^ \wedge + 4\mathop k\limits^ \wedge + \lambda (3i + 4\mathop j\limits^ \wedge - 5\mathop k\limits^ \wedge )$
Hence
Vector $E{q^n}$ of line is
$\Rightarrow \mathop r\limits^ \to = 2\mathop i\limits^ \wedge - 3\mathop i\limits^ \wedge + 4\mathop k\limits^ \wedge + \lambda (3i + 4\mathop j\limits^ \wedge - 5\mathop k\limits^ \wedge )$
Cartesian form is $x\mathop i\limits^ \wedge + y\mathop j\limits^ \wedge - z\mathop k\limits^ \wedge$

= (2 + \lambda )\mathop i\limits^ \wedge + ( - 3 + 4\lambda )\mathop i\limits^ \wedge + (4 - 5\lambda )\mathop k\limits^ \wedge \\\ \Rightarrow x = 2 + \lambda ,y = - 3 + 4\lambda \\\ z = 4 - 5\lambda \\\ \Rightarrow \lambda = x - 2 = \dfrac{{y + 3}}{4} = \dfrac{{z - 4}}{{ - 5}} \\\ \end{gathered} $$ Which is required Cartesian $$E{q^n}$$ of the line **Note:** The cartesian equation for a straight line is $$y{\text{ }} = {\text{ }}mx{\text{ }} + {\text{ }}c,$$ where m represents the gradient of the line, and c is the point where the line crosses the y-axis. A vector equation for a line similarly needs 2 pieces of information: A point on the line. The direction of the line. If the normal vector is normalized (unit length) then the constant term of the plane equation ‘d’ becomes the distance from the origin $$\mathop r\limits^ \to .\mathop n\limits^ \wedge = d\left[ {\mathop n\limits^ \wedge } \right] = 1$$ (normalized).