Question

A line passing through the point of intersection of $x + y = 4$ and $x - y = 2$ makes an angle $\tan^{-1}(\frac{3}{4})$ with the X-axis. It intersects the parabola $y^2 = 4(x - 3)$ at points $(x_1, y_1)$ and $(x_2, y_2)$, respectively. Then $|x_1 - x_2|$ is equal to.

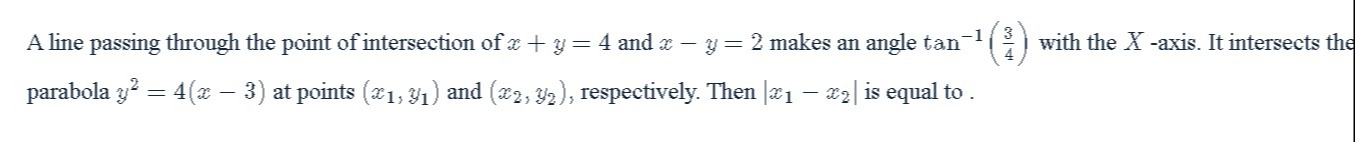
• A. 32/3
• B. 32/9
• C. 8/9
• D. 4/3

Answer 1

Answer: (B)

32/9

Answer 2

Here's how to solve the problem:

1. Find the intersection of the lines:

   Solve the system of equations:

   $$\begin{cases} x + y = 4 \\ x - y = 2 \end{cases}$$

   Adding the equations, we get $2x = 6$, so $x = 3$. Substituting this into the first equation, we get $3 + y = 4$, so $y = 1$. The intersection point is $(3, 1)$.

2. Equation of the line:

   The line passes through $(3, 1)$ with a slope of $m = \tan(\tan^{-1}(\frac{3}{4})) = \frac{3}{4}$. Using the point-slope form, the equation of the line is:

   $$y - 1 = \frac{3}{4}(x - 3) \implies y = \frac{3}{4}x - \frac{5}{4}$$

3. Intersection with the parabola:

   The equation of the parabola is $y^2 = 4(x - 3)$. Substitute $y = \frac{3}{4}x - \frac{5}{4}$ into the parabola equation:

   $$\left(\frac{3}{4}x - \frac{5}{4}\right)^2 = 4(x - 3)$$

   Multiply both sides by 16:

   $$(3x - 5)^2 = 64(x - 3)$$

   Expand and rearrange:

   $$9x^2 - 30x + 25 = 64x - 192 \implies 9x^2 - 94x + 217 = 0$$

4. Find $|x_1 - x_2|$:

   For a quadratic equation $ax^2 + bx + c = 0$, the difference between the roots is given by:

   $$|x_1 - x_2| = \frac{\sqrt{b^2 - 4ac}}{|a|}$$

   In our case, $a = 9$, $b = -94$, and $c = 217$. Compute the discriminant:

   $$D = (-94)^2 - 4 \cdot 9 \cdot 217 = 8836 - 7812 = 1024$$

   Therefore,

   $$|x_1 - x_2| = \frac{\sqrt{1024}}{9} = \frac{32}{9}$$