Question

A line passes through the point of intersection of $2x+y=5$ and $x+3y+8=0$ and parallel to the line $3x+4y=7$ is
1. $3x+4y+3=0$
2. $3x+4y=0$
3. $4x-3y+3=0$
4. $4x-3y=3$

Answer 1

In this problem we need to find the equation of the line which passes through the intersection point of the two lines and also parallel to line $3x+4y=7$. First we will calculate the intersection point of the given lines $2x+y=5$ and $x+3y+8=0$ by solving both the equations. After having the intersection point we will calculate the slope of the line $3x+4y=7$ which will be given by $-\dfrac{a}{b}$ . Now we will use the slope point equation which is $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ to find the required equation.

Complete step by step answer:
Given that, the line passes through the intersection of $2x+y=5$ and $x+3y+8=0$ and parallel to the line $3x+4y=7$.
Considering the equations $2x+y=5$ and $x+3y+8=0$.
Multiplying the equation $x+3y+8=0$ with $2$ and subtracting it from $2x+y=5$, then we will have
$\begin{aligned} & 2x+y-2\left( x+3y+8 \right)=5+0 \\\ & \Rightarrow 2x+y-2x-6y-16=5 \\\ & \Rightarrow -5y=21 \\\ & \therefore y=-\dfrac{21}{5} \\\ \end{aligned}$
Substituting the value of $y$ in the equation $2x+y=5$ to calculate the value of $x$ , then we will get
$\begin{aligned} & 2x-\dfrac{21}{5}=5 \\\ & \Rightarrow 2x=\dfrac{25+21}{5} \\\ & \Rightarrow 2x=\dfrac{46}{5} \\\ & \therefore x=\dfrac{23}{5} \\\ \end{aligned}$
Now the intersection point of the two lines $2x+y=5$ and $x+3y+8=0$ is given by $\left( \dfrac{23}{5},-\dfrac{21}{5} \right)$ .
Considering the line $3x+4y=7$. We know that the slope of the line $ax+by+c=0$ is equal to $-\dfrac{a}{b}$ . Now the slope of the line $3x+4y=7$ is given by
$m=-\dfrac{3}{4}$ .
In the problem they have mentioned that the required line is parallel to the line $3x+4y=7$. So the slope of the require line should be equal to the slope of the line $3x+4y=7$.
Now the equation of the line having slope $m=-\dfrac{3}{4}$ and passing through the point $\left( \dfrac{23}{5},-\dfrac{21}{5} \right)$ from slope point equation is given by
$\begin{aligned} & \left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right) \\\ & \Rightarrow \left( y-\left( -\dfrac{21}{5} \right) \right)=-\dfrac{3}{4}\left( x-\dfrac{23}{5} \right) \\\ & \Rightarrow 4\left( y+\dfrac{21}{5} \right)=-3x+\dfrac{69}{5} \\\ & \Rightarrow 4y+\dfrac{84}{5}+3x-\dfrac{69}{5}=0 \\\ & \Rightarrow 3x+4y+3=0 \\\ \end{aligned}$
So the required line equation is $3x+4y+3=0$ .
The relevant diagram for the solution is given by

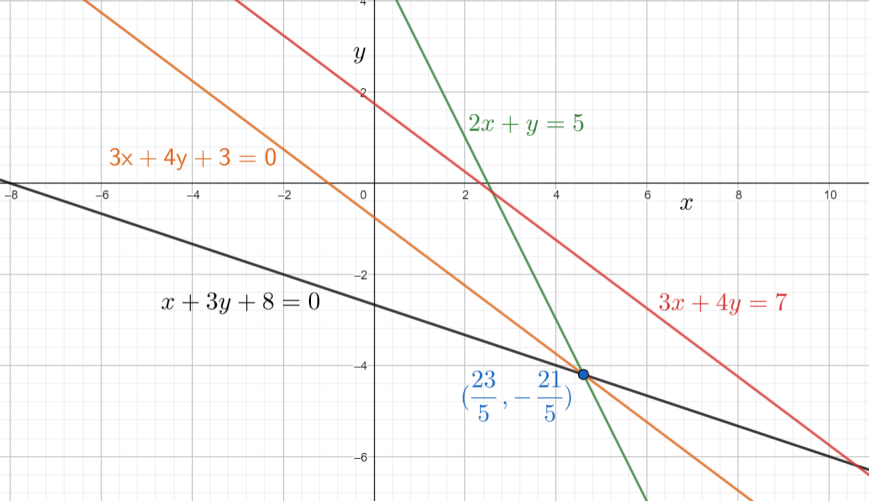
So, the correct answer is “Option 1”.

Note: We can also use another method to find the equation of the required line. The equation of the line which is parallel to the line $ax+by+c=0$ is given by $ax+by+d=0$ . Here substitute the point in the equation $ax+by+d=0$ and find the value of constant $d$ .