Question

A line $L$ is perpendicular to the line $5x - y = 1$ and the area of the triangle formed by the line $L$ and coordinate axes is $5$. The equation of the line $L$ is
\eqalign{ & 1)x + 5y = 5 \cr & 2)x + 5y = \pm 5\sqrt 2 \cr & 3)x - 5y = 5 \cr & 4)x - 5y = \pm 5\sqrt 2 \cr}

Answer 1

It is given that a line is perpendicular to another line whose equation is $5x - y = 1$. Using the slope formula, we can find out the equation of the line $L$ . Then we can substitute the coordinates for the area of the triangle. By doing that, we can find out the coordinates of the line $L$ and hence its equation.
The formula used to solve the question is:
The slope of a line when slope and y-intercept is known is given by, $y = mx + b$
The general equation of a line is $y = mx + c$
Area of triangle, $A = \dfrac{1}{2} \times base \times height$

Complete answer:
The given equation of the line is $5x - y = 1$
Let, the slope of the given line be ${m_1}$ which will be $5$
$\Rightarrow {m_1} = 5$
The slope of the perpendicular line $L = \dfrac{{ - 1}}{5}$
The equation of the line $L,y = \left( {\dfrac{{ - 1}}{5}} \right)x + c$
Multiplying by 5, we get
$x + 5y = 5c$
This is the equation of the line $L$
Let us consider values,
When
\eqalign{ & x = 0,y = c \cr & y = 0,x = 5c \cr}
Therefore, the coordinates will be $(0,c),(0,0) \, and \, (5c,0)$
The given triangle will be as follows:

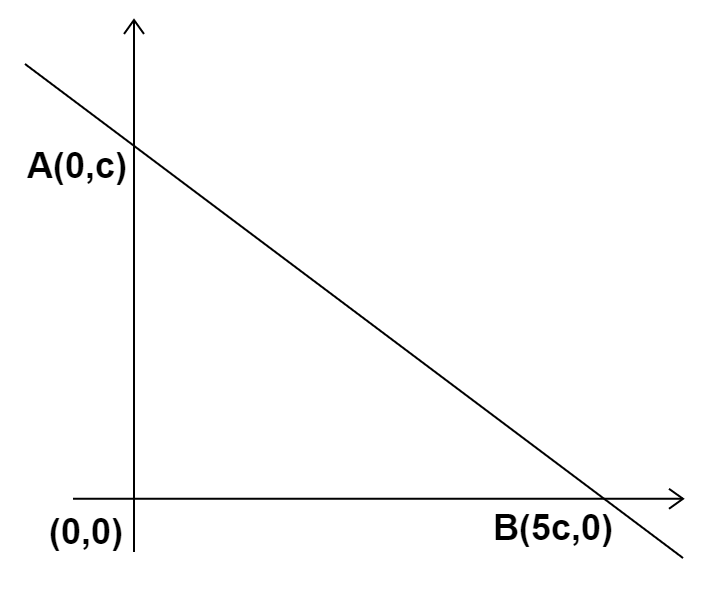
It is given that the area of the triangle is $5$ units.
So, from the above diagram, we have
$\Rightarrow \dfrac{1}{2} \times OB \times OA = 5$
Substituting the values of the coordinates,
\eqalign{ & \Rightarrow \dfrac{1}{2} \times 5c \times c = 5 \cr & \Rightarrow {c^2} = 2 \cr}
Removing the squares on both sides, we get
$c = \pm \sqrt 2$
Now, substituting this value for the equation of line $L$,
$x + 5y = \pm 5\sqrt 2$ which is the final answer.
Hence, option (2) is correct.

Note:
The key words are perpendicular and the area of the triangle. Be careful while constructing the diagram. Use the slope and the line equations while necessary. Also learn the generalized equations properly. While substituting for the area of the triangle, take the coordinates as height and base.