Question

A line is drawn through the point (1,2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin, if the area of the triangle OPQ is least, then the slope of the line PQ is?
A). $-\dfrac{1}{4}$
B). – 4
C). - 2
D). $-\dfrac{1}{2}$

Answer 1

In the above question we will suppose the value of the slope of the line to be “ m” that passes through (1,2) and cuts the coordinate axes at P and Q. Now we will write the equation of the line in one point and slope form and find the points where the line cuts the axes. Then, we will use the method of differentiation to find the minimum value of slope by differentiating the area with respect to “m” and equating it to zero.

Complete step-by-step solution
Let us suppose that the slope of the line is “ m” that passes through the point, say A (1, 2) and cuts the axes at P and Q as shown in the figure below,

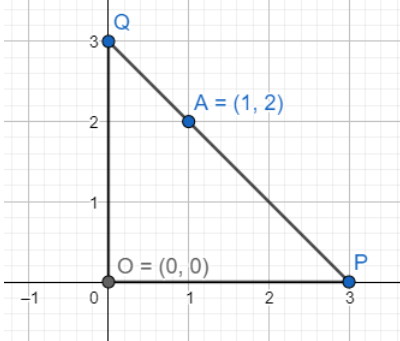
We know that the equation of a line passing through point $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$. So, we can obtain the equation of the line by substituting the points as $y-2=m(x-1)$.
To find the coordinates of P and Q, we know that these points cut the axes. So, point P cuts the x-axis, so it will have y coordinate as 0, substituting y = 0 in the equation of the line, we get

& 0-2=m(x-1) \\\ &\Rightarrow -2=mx-m \\\ &\Rightarrow x=\dfrac{m-2}{m} \\\ &\Rightarrow x=1-\dfrac{2}{m} \\\ \end{aligned}$$ Point Q cuts the y-axis, so it will have x coordinate as 0, substituting x = 0 in the equation of the line, we get $$\begin{aligned} & y-2=m(0-1) \\\ &\Rightarrow y-2=-m \\\ &\Rightarrow y=2-m \\\ \end{aligned}$$ Therefore, we get that the line meets the x-axis at P$$\left( 1-\dfrac{2}{m},0 \right)$$ and y-axis at Q$$\left( 0,2-m \right).$$ Now, we know that coordinates of the ends of triangle OPQ. Since, O is the origin, the distance OP = the x-coordinate = $1-\dfrac{2}{m}$ and the distance OQ = the y-coordinate = $2-m$. We know that the formula of the area of the triangle is given by: $$\text{Area of }\Delta OPQ=\dfrac{1}{2}\times (OP)\times (OQ)$$. Substituting the known values, we get, $$\begin{aligned} & \text{= }\dfrac{1}{2}\times \left| \left( 1-\dfrac{2}{m} \right)\left( 2-m \right) \right| \\\ & =\dfrac{1}{2}\times \left| 2-m-\dfrac{4}{m}+2 \right| \\\ & \text{= }\dfrac{1}{2}\times \left| 4-\left( m+\dfrac{4}{m} \right) \right| \\\ \end{aligned}$$ Now, we will consider the function as $$\text{ }f(m)=\dfrac{1}{2}\left[ 4-\left( m+\dfrac{4}{m} \right) \right]$$. To find the minimum value, we have to differentiate the function first and then equate it to zero, so we get $$\Rightarrow {f}'(m)=\dfrac{1}{2}\left[ -1+\dfrac{4}{{{m}^{2}}} \right]$$. $$\begin{aligned} & \text{Now, }{f}'(m)=0 \\\ & \Rightarrow m=\pm 2 \\\ \end{aligned}$$ Now, we will substitute each critical point at which area is minimum and get $$\begin{aligned} & f(2)=\dfrac{1}{2}\left[ 4-\left( 2+\dfrac{4}{2} \right) \right]=\dfrac{1}{2}\left[ 4-4 \right]=0 \\\ &\Rightarrow f(-2)=\dfrac{1}{2}\left[ 4-\left( -2+\dfrac{4}{-2} \right) \right]=\dfrac{1}{2}\left[ 4-\left( -4 \right) \right]=4 \\\ \end{aligned}$$ Since the area can not be zero, hence the required value of m is – 2. **Therefore, the correct option for the above question is option C.** **Note:** Just be careful while doing calculation as there is a chance that you might make a mistake and you will get the incorrect answer. The mistake that a student can make is while finding the points P and Q and also OP and OQ, so the student must be very careful in that. Also, it is necessary to substitute the critical points and check if the area obtained is positive or negative before finalizing the answer.