Question

A line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ where O is the origin. If the area of the triangle OPQ is least the slope of the line PQ is
$\begin{array}{l} \left( {A.} \right)\,\,\, - 1\\\ \left( B \right)\,\,\,\,\, - 2\\\ \left( C \right)\,\,\,\,\, - \,\,\dfrac{1}{2}\\\ \left( D \right)\,\,\,\,\, - \dfrac{1}{4} \end{array}$

Answer 1

Line is formed when two points are joined. It means a unique line can be drawn through 2 points. And there are infinites lines passing through a given point. Hence in this question it is given that the line is passing through a given point (1, 2). So firstly we can assume the most suitable form for line among 7 forms or line. Here we are using an intercept form $\dfrac{x}{{OQ}} + \dfrac{y}{{OP}} = 1$. Here OQ is the x –intercept and OP is the y intercept. PQ is the required line which makes the intercept with x and y axis. Since x-axis and y-axis are mutually perpendicular axis hence we have a right angle triangle.

Complete step by step solution: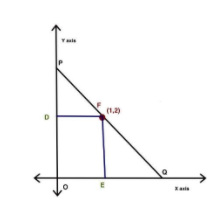
Step 1 From the above figure we can find segment AD by just applying the basic definition of .
$\tan \theta = \dfrac{{perpendicular}}{{base}}$
$\tan \theta = \left( {\dfrac{{PD}}{{DF}}} \right) = \dfrac{{PD}}{1}$
Step 2 from the figure
$\tan \theta = \left( {\dfrac{{EF}}{{EC}}} \right) = \dfrac{2}{{EC}}$

perpendicular = PD + OD\, = \tan \theta + 2\\\ Base\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = OE + EQ\, = 1 + 2\cot \theta \end{array}$$ Step 3 Area of the triangle OPQ is $$\dfrac{1}{2}\left( {2 + \tan \theta } \right)\left( {1 + 2\cot \theta } \right)$$ $$\begin{array}{l} = \dfrac{1}{2}\left( {2 + \tan \theta + 4\cot \theta + 2} \right)\\\ = \dfrac{1}{2}\left( {4 + \tan \theta + 4\cot \theta } \right)\\\ = \dfrac{1}{2}(4 + \ge 4)\\\ = \,\,4 \end{array}$$ Using inequality = In A.M –G.M inequality, equality holds when both numbers in A.P are equal. Here are equal By equating $$\tan \theta \,and\,\cot \theta \,$$we get $$\begin{array}{l} \tan \theta \, = 4\cot \theta \\\ {\tan ^2}\theta = 4\\\ \therefore \,\,\tan \theta = \pm 2 \end{array}$$ $$\begin{array}{l} hence\,slope\,of\,line\,is\,given\,by\,m\,which\,is\,equal\,to\,\tan \theta \\\ and\,\,slope\,of\,line\,is\, \pm 2\\\ but\,only\,\, - 2\,is\,given\,in\,the\,option \end{array}$$ Hence the minimum area of the triangle OPQ is 4 Hence the slope of line is -2 **Note:** In case of triangle related questions and their area. Try to use different trigonometric angles relations like$$\tan \theta ,\cot \theta ,\cos \theta \,etc$$. A.M-G.M tools are often used to calculate the minimum value of the given numbers provided that number should be positive.