Question

A line has intercepted a and b on the coordinate axes. When the axes are rotated, the intercepts become P and q, find the relation between a, b, p and q?

Answer 1

Hint – In this particular type of question use the concept of intercept form of equation of line (i.e. if a line intercepts c and d on the coordinate axis then the equation of line is given as $\dfrac{x}{c} + \dfrac{y}{d} = 1$) and later on in the solution use the concept of angle rotation and basic identity of trigonometric so use these concepts to reach the solution of the question.

Complete step-by-step answer:
Let (a) intercept is on the x-axis and (b) intercept is on y-axis as shown in the figure.
Now as we know that the equation of line in intercept form is given as,
$\Rightarrow \dfrac{x}{a} + \dfrac{y}{b} = 1$...................... (1)
So this is the required equation of line which has intercepts a and b on the coordinate axis.
Now it is given that the coordinate axis is rotated.
Let the coordinate axis be rotated by an angle $\theta$ anti-clockwise as shown in the figure.

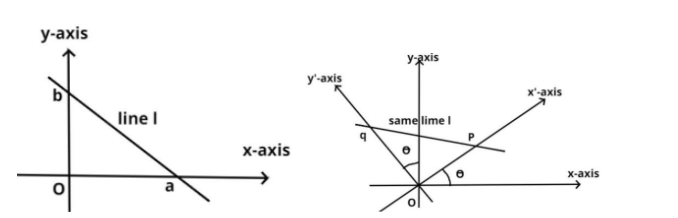
Let the new coordinate axis be x’ and y’ as shown in the figure.
This time a line intercepts become p and q.
So the equation of line become
$\Rightarrow \dfrac{{x'}}{p} + \dfrac{{y'}}{q} = 1$................... (2)
Now from the figure we can say that the angle yox’ are (90 - $\theta$) and the angle y’ox is (90 + $\theta$), because the coordinate axes are always perpendicular to each other (i.e. 90 degree).
Now rotate x axis through $\theta$ in and (90 + $\theta$) in anticlockwise and y axis through (90 - $\theta$) in clockwise and $\theta$ in anti-clockwise we have,
So the new coordinate axis become,
$\Rightarrow x' = x\cos \theta + y\cos \left( {{{90}^o} - \theta } \right)$
As we all know that $\cos \left( {{{90}^o} - \theta } \right) = \sin \theta$
$\Rightarrow x' = x\cos \theta + y\sin \theta$................... (3)
And
$\Rightarrow y' = x\cos \left( {{{90}^o} + \theta } \right) + y\cos \theta$
As we all know that $\cos \left( {{{90}^o} + \theta } \right) = - \sin \theta$ so we have,
$\Rightarrow y' = - x\sin \theta + y\cos \theta$.................... (4)
Now substitute the value of x’ and y’ from equation (3) and (4) in equation (2) we have,
$\Rightarrow \dfrac{{x\cos \theta + y\sin \theta }}{p} + \dfrac{{ - x\sin \theta + y\cos \theta }}{q} = 1$
Now simplify this we have,
$\Rightarrow x\left( {\dfrac{{\cos \theta }}{p} - \dfrac{{\sin \theta }}{q}} \right) + y\left( {\dfrac{{\sin \theta }}{p} + \dfrac{{\cos \theta }}{q}} \right) = 1$................... (5)
Now equation (1) and equation (5) represents the same line so the solution of these equation is given as,
$\Rightarrow \dfrac{{\dfrac{{\cos \theta }}{p} - \dfrac{{\sin \theta }}{q}}}{{\dfrac{1}{a}}} = \dfrac{{\dfrac{{\sin \theta }}{p} + \dfrac{{\cos \theta }}{q}}}{{\dfrac{1}{b}}} = \dfrac{1}{1}$
Now simplify this we have,
$\Rightarrow \dfrac{{\cos \theta }}{p} - \dfrac{{\sin \theta }}{q} = \dfrac{1}{a}$ .................... (6)
And
$\Rightarrow \dfrac{{\sin \theta }}{p} + \dfrac{{\cos \theta }}{q} = \dfrac{1}{b}$...................... (7)
Now squaring and adding equation (6) and (7) we have,
$\Rightarrow {\left( {\dfrac{{\cos \theta }}{p} - \dfrac{{\sin \theta }}{q}} \right)^2} + {\left( {\dfrac{{\sin \theta }}{p} + \dfrac{{\cos \theta }}{q}} \right)^2} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}$
Now open the square we have,
$\Rightarrow \left( {\dfrac{{{{\cos }^2}\theta }}{{{p^2}}} + \dfrac{{{{\sin }^2}\theta }}{{{q^2}}} - 2\dfrac{{\sin \theta \cos \theta }}{{pq}}} \right) + \left( {\dfrac{{{{\sin }^2}\theta }}{{{p^2}}} + \dfrac{{{{\cos }^2}\theta }}{{{q^2}}} + 2\dfrac{{\sin \theta \cos \theta }}{{pq}}} \right) = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}$
$\Rightarrow \dfrac{{{{\cos }^2}\theta }}{{{p^2}}} + \dfrac{{{{\sin }^2}\theta }}{{{q^2}}} + \dfrac{{{{\sin }^2}\theta }}{{{p^2}}} + \dfrac{{{{\cos }^2}\theta }}{{{q^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}$
$\Rightarrow \dfrac{1}{{{p^2}}}\left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right) + \dfrac{1}{{{q^2}}}\left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right) = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}$
Now as we know the basic trigonometric identity i.e. $\left( {{{\sin }^2}\theta + {{\cos }^2}\theta } \right) = 1$ so we have,
$\Rightarrow \dfrac{1}{{{p^2}}} + \dfrac{1}{{{q^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}$
So this is the required relation between a, b, p and q.

Note – Whenever we face such types of question the key concept we have to remember is that the solution of the parallel lines (i.e. slope is same) or the same line (for example ax + by = c and lx + my = n) is given as $\dfrac{a}{l} = \dfrac{b}{m} = \dfrac{c}{n}$ , then first find the equation of line in old as well as new coordinate system as above then use the above solution of same lines and simplify we get the required relation between a, b, p and q.