Question
Question: A line charge of length \(l\) and charge \(Q\) uniformly distributed over the length is placed at a ...
A line charge of length l and charge Q uniformly distributed over the length is placed at a distance r from one edge from a point charge q as shown. Find the force on the point charge:
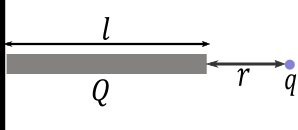
A) 4πε0r(r−l)qQ
B) 4πε0(r−l1)qQ
C) 4πε0(r21−(r+l)21)qQ
D) None of these.
Solution
hint: To solve this type question first we take a small segment of line charge. And assume it as a point charge due to this small segment (small charge) find the force on charge q. In the same manner we calculate force due to every small segment and add them or we can use integration methods to find force due to the whole line charge.We know force between two point charges is given by F=4πε01r2q1q2
Complete step by step solution:
Step 1 : First of all we assume a small segment of length dx on line charge having x distance from point charge q
As given length l having charge Q so the linear charge density given as λ=lQ means charge per unit length
As we can see in diagram
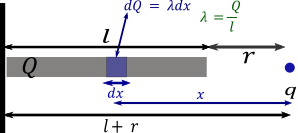
Segment dx having a small charge can be given by dQ=λdx
First we calculate the small force dF on q due to this segment which having charge dQ and distance from q charge is x
Apply formula for force between two point charges F=4πε01r2q1q2
Here q1=dQ and q2=q r=x
⇒dF=4πε01x2qdQ
Segment dx having a small charge can be given by dQ=λdx
⇒dF=4πε01x2qλdx
Rearranging it
⇒dF=4πε0qλx2dx
This is the small force on point charge q due to small segment of dx
Step 2: If we want to calculate total force by l length charge we have to integrate it
Total force due to l length Q charge F can given as
⇒∫dF=4πε0qλr∫l+rx2dx
Net force
⇒F=4πε0qλr∫l+rx−2dx
On integration
⇒F=4πε0qλ[−1x−1]rl+r
⇒F=4πε0qλ[−x1]rl+r
Applying limits
⇒F=4πε0qλ[r1−(l+r)1]
⇒F=4πε0qλ[r(l+r)l+r−r]
⇒F=4πε0qλ[r(l+r)l]
Now put value of linear charge density given byλ=lQ
⇒F=4πε0lqQ(r(l+r)l)
Solving again
⇒F=4πε0r(l+r)qQ
So the total force on the point charge q is ⇒F=4πε0r(l+r)qQ
So option D is correct.
Note: Sometimes students get confused why we use here the limit of integration is r to (r+l). See in diagram the distance between charge and segment of charge vary between r to (r+l) means the closest end of line charge is at distance r and other end of this line charge having (r+l) distance from point charge q .
