Question

A light thread is wound on a disk of mass $m$ in and the other end of the thread is connected to a block of mass $m$, which is placed on a rough ground as shown in diagram. Find the minimum value of coefficient of friction for which block remains at rest.

A. $\dfrac{1}{3}$
B. $\dfrac{1}{4}$
C. $\dfrac{1}{2}$
D. $\dfrac{1}{5}$

Answer 1

Write the equation of motion of the disk to find the tension in the string. For a disk rolling on a surface equation of motion will be, $\tau = {I_{cm}}\alpha$ where, ${I_{cm}} = \dfrac{{m{r^2}}}{2}$ is the moment of inertia along the axis passing through centre of mass $\tau$ is the torque acting on the disk, $\alpha$ is the angular acceleration. Then, find the equation of motion of the block and calculate the coefficient of friction.

Complete step by step answer:
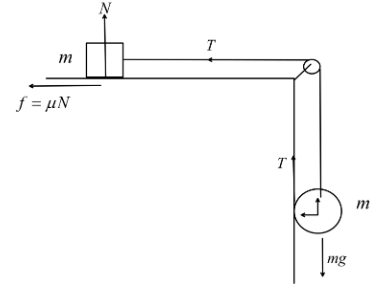
We know that for a body in rotational motion then the equation of motion can be written as, $\tau = I\alpha$ where, $I$ is the moment of inertia along the axis of rotation. $\tau$ is the torque acting on the body, $\alpha$ is the angular acceleration. Here, we have a circular disk of mass $m$ which can roll along the vertical wall. So, the equation of motion can be written as, $\tau = {I_{cm}}\alpha$ where, ${I_{cm}} = \dfrac{{m{r^2}}}{2}$ is the moment of inertia along the axis passing through centre of mass.

Now, we know, angular acceleration is related to linear acceleration as,
${a_{cm}} = \alpha r$
Hence, putting the values we have, $\tau = \dfrac{{m{r^2}}}{2}\dfrac{{{a_{cm}}}}{r}$.
$\tau = \dfrac{{mr{a_{cm}}}}{2}$
Now, we can see that the tension acting on the string is producing the torque on the disk. Hence we can write, $\tau = Tr$
$Tr = \dfrac{{mr{a_{cm}}}}{2}$
$\Rightarrow T = \dfrac{{m{a_{cm}}}}{2}$
Now, we can write the linear equation of motion of the disk as, $mg - T = m{a_{cm}}$.
So, putting the value of tension we get,
$mg = m{a_{cm}} + \dfrac{{m{a_{cm}}}}{2} = \dfrac{{3m{a_{cm}}}}{2}$
$\Rightarrow g = \dfrac{{3{a_{cm}}}}{2}$
$\Rightarrow {a_{cm}} = \dfrac{{2g}}{3}$.
So, tension of the string becomes, $T = \dfrac{m}{2}\dfrac{{2g}}{3} = \dfrac{{mg}}{3}$
Now, we can write the equation of motion of the block at equilibrium(at rest) as, $T - \mu N = 0$ where, $N = mg$.
So, pitting the value of tension we get,
$\dfrac{{mg}}{3} - \mu mg = 0$.
On, simplifying we get, $\mu = \dfrac{1}{3}$.
So, the minimum value of the coefficient of friction must be, $\dfrac{1}{3}$.

Hence, the correct answer is option A.

Note: The frictional force on the block can be greater than $\dfrac{1}{3}mg$ for keeping the block at rest. That means the coefficient of friction can be greater than $\dfrac{1}{3}$ ($\mu \geqslant \dfrac{1}{3}$ ) for the block to be at rest. Though, $f = \dfrac{1}{3}mg$ will be just sufficient to keep the block at rest.