Question

A light string passing over a smooth light pulley connects two blocks of masses a and b (vertically). If the acceleration of the system is $\dfrac{g}{8}$ , then the ratio of the masses is:
A. 9:7
B. 1:2
C. 1:1
D. 5:3

Answer 1

The free-body diagrams of the individual bodies must be drawn and the forces acting on each block must be determined. By equating them using the principle of equilibrium, we can obtain the ratio of their masses.

Complete step by step answer:
Consider a system of pulley with two blocks of masses a and b hanging vertically downwards as shown:

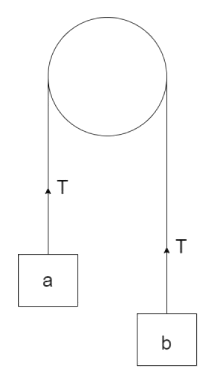
Here, we have to assume that the block b moves further down than the block a. Here, there is tension in the string due to the weight of the block acting downwards.

Let us draw the individual free-body diagrams of the blocks.
Block a:

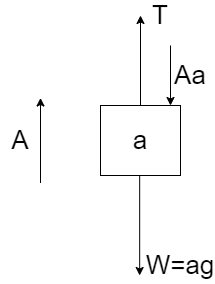
The acceleration of the block is upwards and represented by A.
The forces acting on the body are –
i) Weight equal to mass times the acceleration due to gravity, $W = ag$
ii) Tension in the string acting upwards
iii) Force Aa acting due to the movement of the block, equal to the mass times the acceleration A.
By equilibrium,
$ag + Aa = T$

Block b:

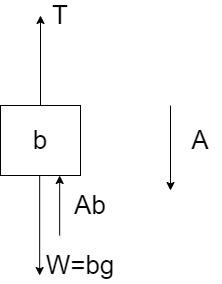
The acceleration of the block is downwards and represented by A.
The forces acting on the body are –
i) Weight equal to mass times the acceleration due to gravity, $W = bg$
ii) Tension in the string acting upwards, T
iii) Force Ab acting due to the movement of the block, equal to the mass times the acceleration A.
By equilibrium,
$T = bg - Ab$
Equating the values of tension,
$ag + Aa = bg - Ab$
The value of acceleration given, $A = \dfrac{g}{8}$
Substituting,
$ag + \dfrac{{ga}}{8} = bg - \dfrac{{gb}}{8}$
$\Rightarrow a + \dfrac{a}{8} = b - \dfrac{b}{8}$
$\Rightarrow \dfrac{7}{8}b = \dfrac{9}{8}a$
$\therefore \dfrac{b}{a} = \dfrac{9}{7}$

Hence, the correct answer is option (A).

Note: Here, in the question it is mentioned as light string and smooth pulley. The reason is that their weights are not considered while solving for the forces in the free-body diagram. In usual cases, the masses of the string and pulley do not affect the calculation of the answer.