Question

A light string passes over a frictionless pulley. To one of its ends a mass of 6kg is attached and to its other end a mass of 10kg is attached. The tension in the string will be

       ![](https://www.vedantu.com/question-sets/afb4b6ae-845a-4469-ae05-5578c1d473234644680594890187910.png)   

A. 50N
B. 75N
C. 100N
D. 150N

Answer 1

In this question, first of all we will draw the free body diagram of the two blocks indicating all the forces acting on each of them. Assuming the acceleration of the 10kg block as ‘a’ In downward direction, we will write the force equation of the two blocks and finally solve the two equations to get acceleration.

Complete answer:
In the question, we have a massless string and a frictionless pulley.
Let the tension in the string be ‘T’ N and the acceleration of the 10 kg mass be ‘a’ in downward direction. Since the two masses are connected by the same string through a frictionless pulley, the acceleration of 6kg mass will also be ‘a’ in upward direction.

The free body diagrams for the two blocks are given below:

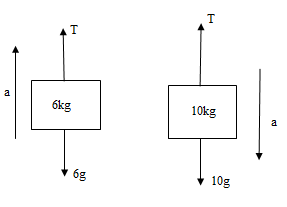
Writing the force equation on the each of two blocks, we get:
10g – T = 10a ……………..(1)
T – 6g = 6a ……………..(2)
On adding equation 1 and 2, we get:
4g = 16a
a =$\dfrac{{4g}}{{16}}$
Putting the value of g = 10, we have:
a = $\dfrac{{4 \times 10}}{{16}} = 2.5m/{s^2}$
putting this value of ‘a’ in equation 1, we get:
10g – T = 102.5 = 25
T = 10g – 25 = 1010 – 25 = 100 – 25 = 75N

So, the correct answer is “Option B”.

Note:
In this question, you should first recognize the different forces acting on each of the masses and then draw the free body diagram for each of them. In case of massless string, the tension is the same everywhere in the string. The force due to gravity of earth always acts in downward direction.