Question

A light rod of length $l$ has two masses ${{m}_{1}}$ and ${{m}_{2}}$attached to its ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
A. $\sqrt{{{m}_{1}}{{m}_{2}}}{{l}^{2}}$
B. $\dfrac{{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}{{l}^{2}}$
C. $\dfrac{{{m}_{1}}+m+2}{{{m}_{1}}{{m}_{2}}}{{l}^{2}}$
D. $({{m}_{1}}+{{m}_{2}}){{l}^{2}}$

Answer 1

Hint: We can do this problem with the help of moment of inertia and the centre of mass equation. We have to find the distance of the masses from the rotational axis by calculating the centre of mass. Then we can add this distance in the formula of the moment of inertia of the system.

Formula used:
$I={{m}_{1}}{{r}_{1}}^{2}+{{m}_{2}}{{r}_{2}}^{2}+.........+{{m}_{n}}{{r}_{n}}^{2}$, where ${{m}_{1}}$, ${{m}_{2}}$,……, ${{m}_{n}}$ are representing the masses of the particles and ${{r}_{1}}$, ${{r}_{2}}$,…………, ${{r}_{n}}$ are representing the distance to the rotation axis of each particle respectively.
${{x}_{cm}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}$

Complete step by step answer:

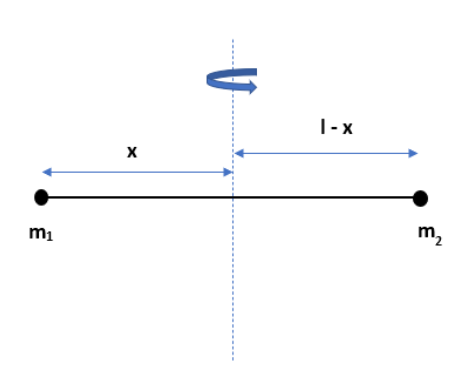
The given light rod of length l has two masses and they are situated at the ends of the rod. We have to find the moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass. As we know, the moment of inertia of any system can be written as,
$I={{m}_{1}}{{r}_{1}}^{2}+{{m}_{2}}{{r}_{2}}^{2}+.........+{{m}_{n}}{{r}_{n}}^{2}$, where ${{m}_{1}}$, ${{m}_{2}}$,……, ${{m}_{n}}$ are representing the masses of the particles and ${{r}_{1}}$, ${{r}_{2}}$,…………, ${{r}_{n}}$ are representing the distance to the rotation axis of each particle respectively.
Here we are considering two masses. So the moment of inertia of our system will contain only two terms.
$I={{m}_{1}}{{r}_{1}}^{2}+{{m}_{2}}{{r}_{2}}^{2}$………………….(1)
Since we are rotating the rod through the centre of mass, we can find out the distance to the rotation axis from the centre of mass equation.
Centre of mass can be written as,
${{x}_{cm}}=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
We can consider the reference as the first mass. Therefore ${{x}_{1}}$ will be zero and ${{x}_{2}}$ will be the length of the rod.
${{x}_{cm}}=\dfrac{{{m}_{1}}\times 0+{{m}_{2}}\times l}{{{m}_{1}}+{{m}_{2}}}$
${{x}_{cm}}=\dfrac{{{m}_{2}}\times l}{{{m}_{1}}+{{m}_{2}}}$
This distance will be the ${{r}_{1}}$.
${{r}_{1}}=\dfrac{{{m}_{2}}l}{{{m}_{1}}+{{m}_{2}}}$………………………(2)
Next, we can find the ${{r}_{2}}$ by subtracting the ${{r}_{1}}$ from the length of the rod.
${{r}_{2}}=l-{{x}_{cm}}=l-\dfrac{{{m}_{2}}l}{{{m}_{1}}+{{m}_{2}}}$
${{r}_{2}}=\dfrac{{{m}_{1}}l}{{{m}_{1}}+{{m}_{2}}}$……………………………..(3)
Now we can plug these equations into the equation (1) to find the moment of inertia of the system.
$I={{m}_{1}}{{\left[ \dfrac{{{m}_{2}}l}{{{m}_{1}}+{{m}_{2}}} \right]}^{2}}+{{m}_{2}}{{\left[ \dfrac{{{m}_{1}}l}{{{m}_{1}}+{{m}_{2}}} \right]}^{2}}$
$I=\dfrac{({{m}_{1}}{{m}_{2}})({{m}_{1}}+{{m}_{2}}){{l}^{2}}}{{{({{m}_{1}}+{{m}_{2}})}^{2}}}$
$I=\dfrac{({{m}_{1}}{{m}_{2}}){{l}^{2}}}{{{m}_{1}}+{{m}_{2}}}$
Therefore, the correct answer is option B.

Note: If we are doing this problem without finding the centre of mass and directly input the distance as $x$ and $(l-x)$ will lead to the wrong answer. To find the centre of mass we have to consider a point as a reference point. That’s why we are getting the ${{x}_{1}}$ as zero. Candidates are advised to do these kinds of problems with the help of a diagram to understand easily.