Question

A light rod of length l and with a mass m attached to its end is suspended vertically. It is turned through ${{180}^{\circ }}$ and then released. Calculate the speed of mass and the tension in the rod when the mass reaches at the lowest point. If the system is released with the rod horizontal, at what angle from the vertical the tension in the rod would be equal to the weight of the body.

Answer 1

Use the law of conservation of energy and find the velocity of the mass when it reaches at the lowest point. Then the formula for the centripetal acceleration and calculate the tension in the rod at this point. Then by using the same two concepts find the angle that the rod makes with the vertical when the tension is equal to the weight of the rod.
Formula used:
$\Delta K=-\Delta U$
$\Delta U=mg\Delta h$
$K=\dfrac{1}{2}m{{v}^{2}}$
${{a}_{c}}=\dfrac{{{v}^{2}}}{r}$
${{F}_{net}}=ma$

Complete answer:
When the rod is rotated by ${{180}^{\circ }}$ and released, it will come down in a rotational motion under the influence of gravity. Let us assume that the rod is masseless. Therefore, the gravity will only affect the motion of the mass.
Let's use the law of conservation of energy, which says that the change in kinetic energy of a mass is equal to the negative of the change in the potential energy.
i.e.$\Delta K=-\Delta U$.
When the rod is rotated by an angle of ${{180}^{\circ }}$, the mass is at a height 2l above the lowest level. When a mass m comes down from a height h, its gravitational potential energy decreases by an amount of mgh, where g is acceleration due to gravity.
In this case, the mass m comes down from a height of 2l. Therefore, the change in gravitational potential energy is $\Delta U=-mg(2l)=-2mgl$.
The change in kinetic energy of the mass is $\Delta K=\dfrac{1}{2}m{{v}^{2}}$.
Therefore,
$\Rightarrow \dfrac{1}{2}m{{v}^{2}}=-(-2gml)$
$\Rightarrow {{v}^{2}}=4gl$
$\Rightarrow v=\pm 2\sqrt{gl}$
Speed is always positive. Therefore, $\Rightarrow v=2\sqrt{gl}$.
This means that the speed of the mass at the lowest point is $2\sqrt{gl}$.
At the lowest the mass will have a centripetal acceleration which is given as ${{a}_{c}}=\dfrac{{{v}^{2}}}{r}$, where r is the radius of the circular path. The centripetal acceleration is always towards the point of rotation.
In this case, r = l.
Therefore,
${{a}_{c}}=\dfrac{{{v}^{2}}}{l}$
Substitute the value of ${{v}^{2}}$.
${{a}_{c}}=\dfrac{4gl}{l}=4g$ …. (i)
Let's draw the free body diagram of the mass at the lowest point as shown.

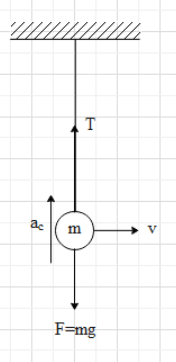
From the diagram we know that the net force on the mass is ${{F}_{net}}=T-mg$.
And we know that ${{F}_{net}}=ma$.
$\Rightarrow T-mg=m{{a}_{c}}$.
Substitute the value of ${{a}_{c}}$ from (i).
$\Rightarrow T-mg=m(4g)$
$\Rightarrow T=5mg$
This means that the tension in the rod at the lowest point is 5mg.
Suppose when the tension is equal to the weight of the body, the angle made by the rod with the vertical be $\theta$.
At this time, the mass will have a centripetal acceleration along the length of the rod. Let us find the net force on the rod.

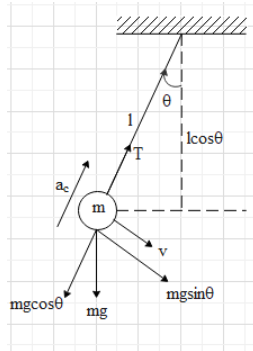
From the figure, we get to know that the net force along the length of the rod is $T-mg\cos \theta$ .
Therefore,
$T-mg\cos \theta =m{{a}_{c}}$
$\Rightarrow T-mg\cos \theta =m\dfrac{{{v}^{2}}}{l}$.
And T=mg.
$\Rightarrow mg-mg\cos \theta =m\dfrac{{{v}^{2}}}{l}$ ….. (ii).
We can find the value of ${{v}^{2}}$ with the law of conservation of energy.
At this time, the rod has come down from a height of $l\cos \theta$. Therefore,
$\Delta U=-mg(l\cos \theta )$.
And $\Delta K=\dfrac{1}{2}m{{v}^{2}}$
But, $\Delta K=-\Delta U$
This means that $\dfrac{1}{2}m{{v}^{2}}=-\left( -mg(l\cos \theta ) \right)$.
$\Rightarrow \dfrac{1}{2}m{{v}^{2}}=mg(l\cos \theta )$
$\Rightarrow {{v}^{2}}=2gl\cos \theta$
Substitute this value in (ii).
$\Rightarrow mg-mg\cos \theta =m\dfrac{2gl\cos \theta }{l}$
$\Rightarrow 1-\cos \theta =2\cos \theta$
$\Rightarrow \cos \theta =\dfrac{1}{3}$
$\Rightarrow \theta ={{\cos }^{-1}}\dfrac{1}{3}$

Note:
Other than the law of conservation of energy, we can also use the work energy theorem. According to the work energy theorem, the change in kinetic energy of a body is equal to the total work done on the body.
Note that only the gravitational force does a work on the mass. However, the tension in the rod keeps the mass in circular motion.