Question

A light rod of length is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section and the other of brass of cross-section . Along the rod at what distance a weight may be hung to produce equal stresses in both the wires.

$({Y_{steel}} = 2 \times {10^{11}}N{m^{ - 2}},{Y_{brass}} = 1 \times {10^{11}}N{m^{ - 2}})$
(a)$\dfrac{4}{3}m$from steel wire
(b)$\dfrac{4}{3}m$from brass wire
(c)$1m$from steel wire
(d)$\dfrac{1}{4}m$from brass wire

Answer 1

In order to calculate the distance a weight may be hung to produce equal stresses in both the wires, we need to refer to the following image. Also, the formula of stress and strain is required.

      ![](https://www.vedantu.com/question-sets/ac4aee46-b4f5-44e1-987d-5ac57861b7399140203946144537276.png)  

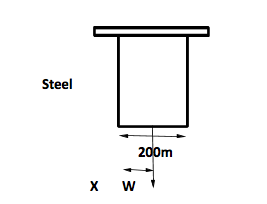
As per the situation is as shown in the figure,

Let a weight $W$be suspended at a distance $x$from steel wire. Let ${{T}_{S}}$and ${{T}_{B}}$ be tensions in the steel and brass wires respectively.
So, Stress in steel wire$=\dfrac{{{T}_{S}}}{{{A}_{S}}}$
Stress in brass wire $=\dfrac{{{T}_{B}}}{{{A}_{B}}}$
Now, for equal stress in both the wires
$\dfrac{{{T}_{B}}}{{{A}_{B}}}=\dfrac{{{T}_{B}}}{{{A}_{B}}}$
$\dfrac{{{T}_{B}}}{{{T}_{B}}}=\dfrac{{{A}_{S}}}{{{A}_{B}}}=\dfrac{0.1c{{m}^{2}}}{0.2c{{m}^{2}}}=\dfrac{1}{2}$………(i)
for the rotational equilibrium of the rod,
${{T}_{S}}x={{T}_{B}}(2-x)$
$\dfrac{2-x}{x}=\dfrac{{{T}_{S}}}{{{T}_{B}}}=\dfrac{1}{2}$ [Using (i)]
$4-2x=x\text{ }or\text{ }3x=4~or~x=\dfrac{4}{3}m$from the steel wire.

Hence, the answer to this question is option (a).

Additional Information: In mechanics, stress is defined as a force applied per unit area. The strain is the amount of deformation experienced by the body in the direction of force applied, divided by initial dimensions of the body. The relation for deformation in terms of length of a solid is given below.

Note: While solving this question, we should be aware of the different types of formula used here. The formulae are basically from stress and strain and how the different values of the variable of the formula is used from the question. The formula is modified and used here to take out the required solution for the problem given here. Different formulae are used here which must be taken into consideration while solving the question. The figure provided here must be observed carefully and study the case here.