Question

A light ray strikes a flat glass plate, at a small angle $'\theta '$. The glass plate has thickness $'t'$ and refractive index $'\mu '$. What is the lateral displacement $'d'$?
A) $\dfrac{{t\theta (\mu + 1)}}{\mu }$
B) $\dfrac{{t\theta (\mu - 1)}}{\mu }$
C) $\dfrac{t}{{\theta \mu }}(\mu - 1)$
D) $\dfrac{\mu }{{t\theta }}(\mu + 1)$

Answer 1

Just keep in mind that the lateral displacement is defined as the path which is traced by incident radiation and the path traced by an emergent ray when the ray comes out of the glass slab. Here, we will calculate the lateral displacement by using the suitable formula.

Formula used:
The formula used for calculating lateral displacement is given by
$d = t\left[ {1 - \dfrac{{\cos \theta }}{{\sqrt {{\mu ^2} - {{\sin }^2}\theta } }}} \right]\sin \theta$
Where, $d$ is the lateral displacement
$t$ is the thickness of the glass slab
$\theta$ is the angle at which the light ray strikes
$\mu$ is the refractive index

Complete step by step solution:
As we all know, the lateral displacement is given by
$d = t\left[ {1 - \dfrac{{\cos \theta }}{{\sqrt {{\mu ^2} - {{\sin }^2}\theta } }}} \right]\sin \theta$
Now, as given in the question, $\theta$ is very small, which means that
$\cos \theta \simeq 1$ and $\sin \theta \simeq 1$
Therefore, the above equation becomes
$d = t\left[ {1 - \dfrac{1}{{\sqrt {{\mu ^2} - {\theta ^2}} }}} \right]\theta$
Now, let $\theta \to 0$ with respect to $\mu$, therefore the above equation becomes
$d = t\left[ {1 - \dfrac{1}{\mu }} \right]\theta$
On further solving, we have
$\Rightarrow \,d = t\left( {\dfrac{{\mu - 1}}{\mu }} \right)\theta$
$\Rightarrow \,d = t\theta \left( {\dfrac{{\mu - 1}}{\mu }} \right)$
Which is the value of lateral displacement.

Hence, option (B) is the correct option.

Additional Information:
Now, let us derive the formula of lateral displacement used above.
For this we will draw a diagram showing light incidents on glass.

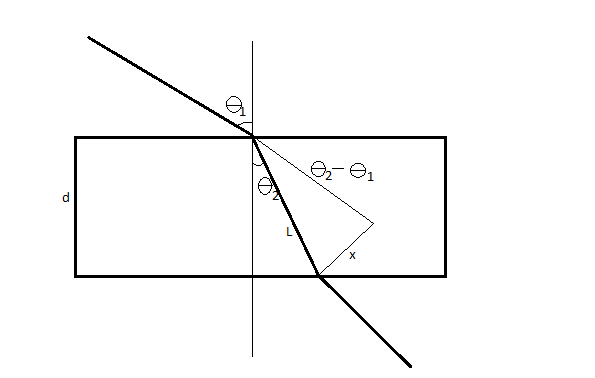
From the triangles shown in the figure, we can say that
$\dfrac{x}{L} = \sin ({\theta _1} - {\theta _2})$
$\Rightarrow \dfrac{x}{L} = \sin {\theta _1}\cos {\theta _2} - \cos {\theta _1}\sin {\theta _2}$
And $\dfrac{t}{L} = \cos {\theta _2}$
As we know, $\cos \theta = \sqrt {1 - {{\sin }^2}\theta }$
Now, combining the above equations we get,
$x = \dfrac{t}{{\cos {\theta _2}}}(\sin {\theta _1}\cos {\theta _2} - \cos {\theta _1}\sin {\theta _2})$
Now, the above equation becomes
$x = t\left( {\sin {\theta _1} - \dfrac{{\sin {\theta _2}\cos {\theta _1}}}{{\cos {\theta _2}}}} \right)$
Now, as we know,
$n = \dfrac{{\sin {\theta _1}}}{{\sin {\theta _2}}}$
$\Rightarrow \,\sin {\theta _2} = \dfrac{{\sin {\theta _1}}}{n}$
Therefore, putting the value of $\sin {\theta _2}$, we get
$x = t\left( {\sin {\theta _1} - \dfrac{{\sin {\theta _1}\cos {\theta _1}}}{{n\cos {\theta _2}}}} \right)$
Now, putting the value of $\cos \theta$ , we get
$x = t\left( {\sin {\theta _1} - \dfrac{{\sin {\theta _1}\sqrt {1 - {{\sin }^2}{\theta _1}} }}{{n\sqrt {1 - {{\sin }^2}{\theta _2}} }}} \right)$
Now, putting the value of $\sin {\theta _2}$
$x = t\left( {\sin {\theta _1} - \dfrac{{\sin {\theta _1}\sqrt {1 - {{\sin }^2}{\theta _1}} }}{{n\sqrt {1 - \dfrac{{{{\sin }^2}{\theta _1}}}{{{n^2}}}} }}} \right)$
$\Rightarrow \,x = t\sin {\theta _1}\left( {1 - \dfrac{{\sqrt {1 - {{\sin }^2}{\theta _1}} }}{{\sqrt {{n^2} - {{\sin }^2}{\theta _1}} }}} \right)$
Which is the expression of lateral displacement.

Note: Now we will discuss the factors on which the lateral displacement depends which are given below:
1. The thickness of the glass slab.
2. Refractive index of the glass slab.
3. The angle at which incident ray enters the glass slab.