Question
Question: A light ray is incident on a plane mirror, which after getting reflected strikes another plane mirro...
A light ray is incident on a plane mirror, which after getting reflected strikes another plane mirror, as shown in figure. The angle between the two mirrors is 60∘. Find the angle θ is shown in figure.
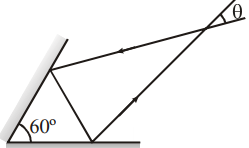
Solution
Hint : In this question, we will use angle sum property. A triangle containing three angles and three sides and a pair of neighbouring sides bound each vertex. In a Euclidean period, the sum of triangle angles equals 180 degrees. It does not matter if the triangle is obtuse, an acute, or a right triangle; the sum of all angles will be 180 degrees. Thus, the angle sum property says that the sum of the triangle angles is equal to 180 degrees.
Complete step-by-step solution:
The angle between the two mirrors is 60∘.
Let ∠A=2x
∠B=2y
This gives,
∠OAB=90∘−x
∠OBA=90∘−y
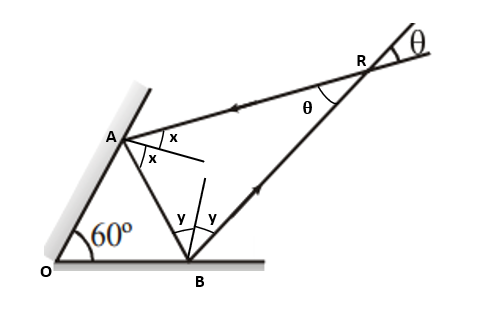
In triangle OAB,
Using sum of angle property,
60∘+(90∘−x)+(90∘−y)=180∘
⟹60∘−x−y=0
⟹x+y=60∘
Now, we will apply sum of angle property,
θ+2x+2y=180∘
Put x+y=60∘ in above formula:
θ+2(60∘)=180∘
⟹θ=180–120=60∘
Hence, the angle θ is 60∘.
Note: A mirror is a reflective covering that light does not move through but bounces off, producing an image. Mirrors are formed by putting a thin coating of silver nitrate or aluminium following a smooth piece of glass. When we place an object in the face of a mirror, we see the identical object in the mirror.
