Solveeit Logo
Login

Question

Question: A light beam is travelling from Region I to Region IV (refer figure). The refractive indices in regi...

A light beam is travelling from Region I to Region IV (refer figure). The refractive indices in region I, II, III and IV are n0{{n}_{0}}, n0/2{{n}_{0}}/2, n0/6{{n}_{0}}/6 and n0/8{{n}_{0}}/8, respectively. The angle of incidence θ\theta for which the beam just misses entering region IV is

A) sin⁡−1(3/4)A)\ {{\sin }^{-1}}\left( 3/4 \right)
B) sin⁡−1(1/8)B)\ {{\sin }^{-1}}\left( 1/8 \right)
C) sin⁡−1(1/4)C)\ {{\sin }^{-1}}\left( 1/4 \right)
D) sin⁡−1(1/3)D)\ {{\sin }^{-1}}\left( 1/3 \right)

Explanation

Solution

This problem can be solved by realizing that if the beam just misses entering the region IV, then the angle of incidence for the ray at the interface of region III and region IV must be the critical angle, the relation for which we can find out using Snell’s law for the preceding regions.

Formula used:
θC=sin⁡−1(n2n1){{\theta }_{C}}={{\sin }^{-1}}\left( \dfrac{{{n}_{2}}}{{{n}_{1}}} \right)
n1sin⁡θ1=n2sin⁡θ2{{n}_{1}}\sin {{\theta }_{1}}={{n}_{2}}\sin {{\theta }_{2}}

Complete step-by-step answer:
For the light ray to not enter the region IV which has a lower refractive index than region III, it must be internally reflected at the interface at the critical angle.
Let us draw a proper diagram to illustrate this.

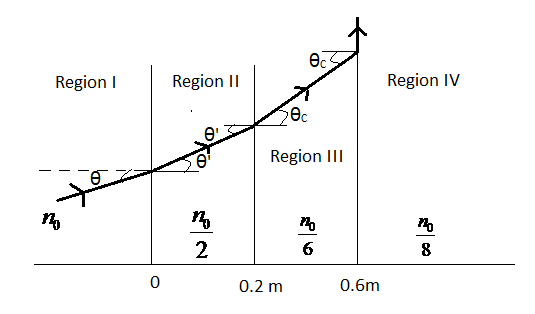
We have marked the angles and used the geometry and properties of alternate interior angles in doing so.
Now, according to Snell’s Law when light goes from a medium of refractive index n1{{n}_{1}} to a medium of refractive index n2{{n}_{2}}, the angle of incidence θ1{{\theta }_{1}} is related to the angle of refraction θ2{{\theta }_{2}} as
n1sin⁡θ1=n2sin⁡θ2{{n}_{1}}\sin {{\theta }_{1}}={{n}_{2}}\sin {{\theta }_{2}} --(1)
Also the critical angle θC{{\theta }_{C}} for total internal reflection, when light goes from an optically denser medium of refractive index n1{{n}_{1}} to an optically rarer medium of refractive index n2{{n}_{2}} is given by
θC=sin⁡−1(n2n1){{\theta }_{C}}={{\sin }^{-1}}\left( \dfrac{{{n}_{2}}}{{{n}_{1}}} \right) --(2)
Now, coming back to the question, when light goes from region I to region II, using (1), we get
n0sin⁡θ=n02sin⁡θ′{{n}_{0}}\sin \theta =\dfrac{{{n}_{0}}}{2}\sin \theta '
∴sin⁡θ=12sin⁡θ′\therefore \sin \theta =\dfrac{1}{2}\sin \theta '
∴sin⁡θ′=2sin⁡θ\therefore \sin \theta '=2\sin \theta --(3)
Now, when the light goes from region II to region III, using (1), we get
n02sin⁡θ′=n06sin⁡θC\dfrac{{{n}_{0}}}{2}\sin \theta '=\dfrac{{{n}_{0}}}{6}\sin {{\theta }_{C}}
∴sin⁡θ′=13sin⁡θC\therefore \sin \theta '=\dfrac{1}{3}\sin {{\theta }_{C}}
∴sin⁡θC=3sin⁡θ′\therefore \sin {{\theta }_{C}}=3\sin \theta ' --(4)
Now, using (2), we get
θC=sin⁡−1(n08n06)=sin⁡−1(68)=sin⁡−1(34){{\theta }_{C}}={{\sin }^{-1}}\left( \dfrac{\dfrac{{{n}_{0}}}{8}}{\dfrac{{{n}_{0}}}{6}} \right)={{\sin }^{-1}}\left( \dfrac{6}{8} \right)={{\sin }^{-1}}\left( \dfrac{3}{4} \right)
∴sin⁡θC=34\therefore \sin {{\theta }_{C}}=\dfrac{3}{4} --(5)
Putting (5) in (4), we get
34=3sin⁡θ′\dfrac{3}{4}=3\sin \theta ' --(6)
Putting (3) in (6), we get
34=3(2sin⁡θ)\dfrac{3}{4}=3\left( 2\sin \theta \right)
∴sin⁡θ=18\therefore \sin \theta =\dfrac{1}{8}
∴θ=sin⁡−1(18)\therefore \theta ={{\sin }^{-1}}\left( \dfrac{1}{8} \right)
Therefore, the required value of θ\theta is sin⁡−1(18){{\sin }^{-1}}\left( \dfrac{1}{8} \right).
Therefore, the correct option is B) sin⁡−1(1/8)B)\ {{\sin }^{-1}}\left( 1/8 \right).

Note: Students might get confused upon seeing the lengths of the region in the figure given in the question. However, they must understand that the critical angle and in general the angles of incidence and refraction have nothing to do with the lengths of the medium but only depend upon their refractive indices. The lengths are given just to confuse students who are not clear with their concepts and make them feel nervous about attempting the question.