Question

A lift is moving downwards with an acceleration equal to the acceleration due to gravity. A body of mass $M$ kept on the floor of the lift is pulled horizontally. If the coefficient of friction is $\mu$ , then the frictional resistance offered by the body is
A. $Mg$
B. $\mu Mg$
C. $2\mu Mg$
D. zero

Answer 1

Here the reference frame is the lift which is moving downwards with an acceleration equal to the acceleration due to gravity. This becomes a non-inertial frame of reference. So, the concept of pseudo force will be used here. We shall first draw the free body diagram of the mass $M$ indicating all the forces and then equate the vertical forces to get the value of the normal reaction. Then we shall substitute the value of normal reaction obtained in the equation $f_r = \mu N$ where $\mu$ is the coefficient of friction and $f_r$ is the frictional force acting.

Complete step by step answer:
Let’s first visualize the situation.

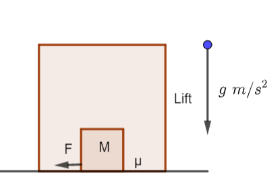
The free body diagram for the mass $M$ will be

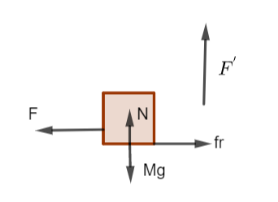
Here F is applied horizontal force, fr is the frictional resistance offered to the motion caused due to the force applied, N is the normal reaction of the body and ${F^1}$ is the fictitious force or the pseudo force due to the moving lift.

The pseudo force is given by ${F^1} = Mg$ since the lift is moving downwards with an acceleration equal to the acceleration due to gravity.
Equating forces in the vertical direction,
$N + {F^1} = Mg$
$\Rightarrow N + Mg = Mg$
$\Rightarrow N = 0$
Now we know that the frictional force is directly proportional to the normal reaction and is given by
$f_r = \mu N$
where $\mu$ is the coefficient of friction.
Since $N = 0$ , the frictional force will also be zero.

Hence, option D is the correct answer.

Note: Pseudo force acts in the direction opposite to the motion of the frame of reference. It counteracts the effect produced by the motion of the reference frame and hence we need not include the variables related to the moving frame in the force equations. It is a fictitious force and does not exist in reality. The problems involving moving frames could be solved without using this concept also. But the number of equations increases and it becomes a cumbersome process.