Question

A letter A is constructed of a uniform wire of resistance $1\text{ }\Omega \text{/cm}$ . The sides of the letter are $\text{20 cm}$ and the cross piece in the middle is $\text{10 cm}$ long. The resistance between the ends of the legs will be:
(A) $\text{32}\text{.4 }\Omega$
(B) $28.7\text{ }\Omega$
(C) $2\text{6}\text{.7}\Omega$
(D) $2\text{4}\text{.7 }\Omega$

Answer 1

To find the resistance between the ends of the legs as directed in the question, we need to arrange the given setup into a combination of series and parallel resistances and before doing that, we need to find the resistance of each part of the circuit. To this use, we have been given the resistance per unit length of the wire of the resistances. Let’s dive in and see how it’s done.

Formula Used:
${{\operatorname{R}}_{series}}=R_1+R_2$
$\dfrac{1}{{{\text{R}}_{parallel}}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}$

Complete step by step answer:
We have been given the resistance per unit length and the lengths of different parts of the alphabet.
Now the length of the cross piece in the middle is $\text{10 cm}$ and the other two sides of the letter are $\text{20 cm}$ each. Now the cross piece divides the arms of the letter in two equal parts, and as such, the resistance of each unit can be given as $r=\text{ }1\text{ }\Omega \text{/cm}\times 10cm=10\Omega$ .
The resistance of the arms forming the sides of the triangle in the letter A will be in series with each other and their equivalent resistance will be in parallel to the base of the triangle forming the triangle. Now once we resolve this resistance, the resistance of the two legs of our arrangement will be in series with this equivalent resistance.
Maybe you didn't quite catch that with all the fancy words and the maze-like paragraphs. Let me help you visualize it with the help of the following figure.

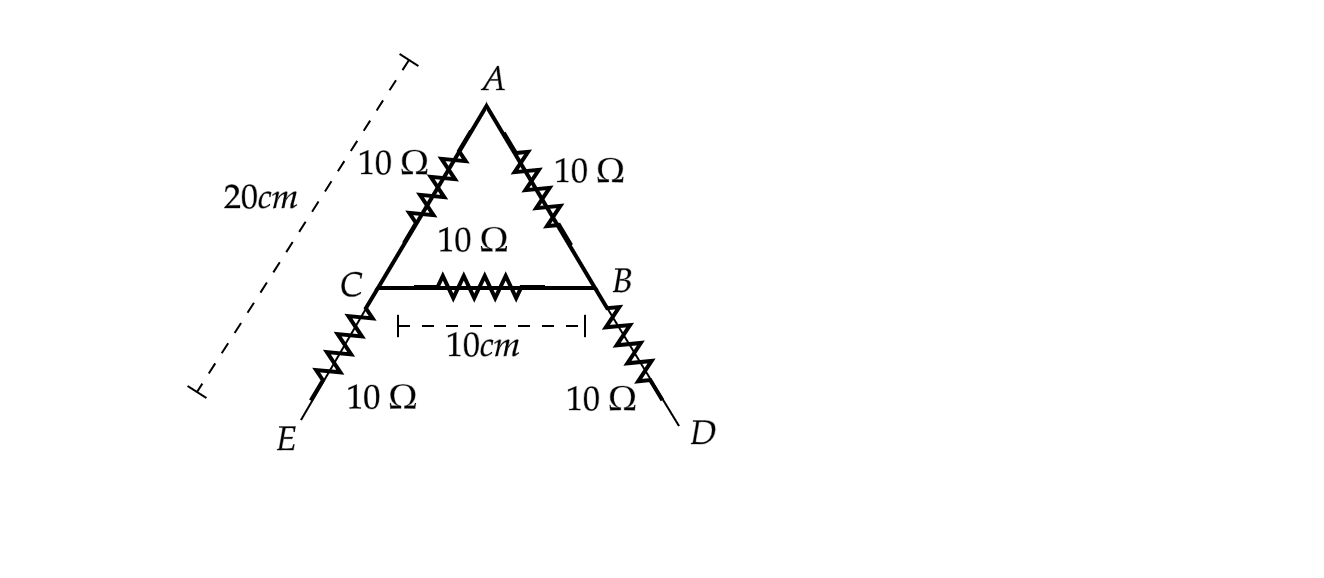
The piece AC is in series with AB and their equivalent resistance will be in parallel to BC. If the net equivalent of all these three resistances has a certain value. Then the resistance of that value will be in series with the pieces CE and BD. This diagram depicts the essence of the above paragraphs.
Moving ahead, we’ll start resolving the circuit.
For the arms AC and AB, equivalent resistance $(R'')=r+r$ where $r=10\Omega$
Hence $R''=10\Omega +10\Omega =20\Omega$
The equivalent resistance of $R''$ and the arm BC $(\dfrac{1}{R'})=\dfrac{1}{R''}+\dfrac{1}{r}$ where $R''=20\Omega$ and $\text{r=}10\Omega$

& (\dfrac{1}{R'})=\dfrac{1}{R''}+\dfrac{1}{r} \\\ & \Rightarrow \dfrac{1}{R'}=\dfrac{1}{20}+\dfrac{1}{10} \\\ & \Rightarrow R'=\dfrac{20}{3}\Omega =6.67\Omega \\\ \end{aligned}$$ Now, this resistance $$R'$$ is in series with the arms CE and BD. Hence equivalent resistance of the circuit $$(R)=2r+R'$$ where $$R'=6.67\Omega $$ and $$\text{r=}10\Omega $$ Hence, $$\begin{aligned} & R=(20+6.67)\Omega =26.67\Omega \\\ & \Rightarrow R\approx 26.7\Omega \\\ \end{aligned}$$ This is the resistance between the legs and we can now say that (C) is the correct option. **Note:** Our answer depends upon which points we choose to find the equivalent resistance. Here we were told to find the resistance across the legs and hence we choose the points D and E as our endpoints. Many students make the wrong choice with the endpoints and end up with the wrong answers despite doing all the right calculations. To avoid such mistakes, read the question properly, at least twice.