Question

A letter ‘A’ is constructed of a uniform wire of resistance $1\,ohm/cm$. The sides of the letter are $20\,{\text{cm}}$ long and cross piece in the middle is $10\,{\text{cm}}$ long while the vertex angle is $60^\circ$. The resistance of the letter between the two ends of the legs is:
A. $\dfrac{{40}}{3}\,\Omega$
B. $\dfrac{{80}}{3}\,\Omega$
C. $40\,\Omega$
D. $10\,\Omega$

Answer 1

First determine the length of the each part of the wire used to construct letter A. From these lengths, determine the resistance of all the resistance in the letter A. Then draw the equivalent circuit diagram of the circuit formed using resistances in the letter A. Then calculate the net resistance in the circuit using the formula for equivalent resistance of the resistors in series and parallel arrangement.

Formulae used:
The equivalent resistance ${R_{eq}}$ of the two resistors ${R_1}$ and ${R_2}$ connected in series is
${R_{eq}} = {R_1} + {R_2}$ …… (1)
The equivalent resistance ${R_{eq}}$ of the two resistors ${R_1}$ and ${R_2}$ connected in parallel is
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ …… (2)

Complete step by step answer:
We have given that the letter ‘A’ is constructed using a uniform wire of resistance $1\,ohm/cm$.
$\dfrac{R}{L} = 1\,ohm/cm$
The length of the sides of the letter is $20\,{\text{cm}}$ and the length of the cross piece in the middle is $10\,{\text{cm}}$. We have asked to calculate the resistance between the two ends of the legs of letter A. Let us first draw the diagram of the letter A with a simplified equivalent circuit diagram.

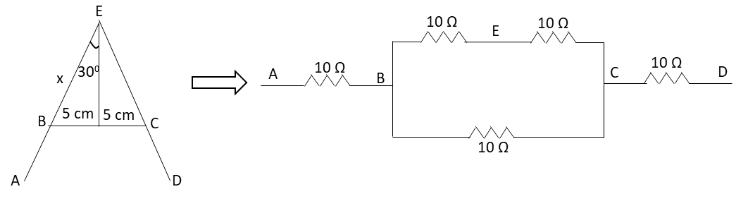
From the above diagram, let us find out the value of x. According to the trigonometric relations, we can write
$\sin 30^\circ = \dfrac{5}{x}$
$\Rightarrow \dfrac{1}{2} = \dfrac{5}{x}$
$\Rightarrow x = 10\,{\text{cm}}$
From the above diagram, we can also write
${\text{AB}} = {\text{CD}} = {\text{AE}} - x$
$\Rightarrow {\text{AB}} = {\text{CD}} = \left( {20\,{\text{cm}}} \right) - \left( {10\,{\text{cm}}} \right)$
$\Rightarrow {\text{AB}} = {\text{CD}} = 10\,{\text{cm}}$
The length of every distinct part used in the letter A is the same which is $10\,{\text{cm}}$.
The resistance of the resistances in the wire is
$\dfrac{R}{{10\,{\text{cm}}}} = 1\,{\text{ohm/cm}}$
$\Rightarrow R = 10\,\Omega$
Hence, the resistance of each resistance in every part of the letter A is $10\,\Omega$.
Let us first determine the equivalent resistance between the points B and C.The equivalent resistance of the upper two resistance according to equation (1) is
$R' = 10\,\Omega + 10\,\Omega$
$\Rightarrow R' = 20\,\Omega$
The net resistance across the points B and C according to equation (2) is
$\dfrac{1}{{{R_{BC}}}} = \dfrac{1}{{10\,\Omega }} + \dfrac{1}{{20\,\Omega }}$
$\Rightarrow {R_{BC}} = \dfrac{{200}}{{30}}$
$\Rightarrow {R_{BC}} = \dfrac{{20}}{3}\,\Omega$
Hence, the equivalent resistance between the points B and C is $\dfrac{{20}}{3}\,\Omega$.
Now the net resistance in the whole circuit is
${R_{eq}} = 10\,\Omega + \dfrac{{20}}{3}\,\Omega + 10\,\Omega$
$\therefore {R_{eq}} = \dfrac{{80}}{3}\,\Omega$
Therefore, the resistance of the letter between the two ends of the legs is $\dfrac{{80}}{3}\,\Omega$.

Hence, the correct option is B.

Note: The students should keep in mind that we have given the value of resistance per unit length and not the resistance of the wire used. Also there are different parts of the wire formed for the construction of the letter A and the resistances for the different parts are considered differently which has the same value as the lengths of the different parts of the wire is the same.