Question

A lens having focal length f and aperture of the diameter d forms an image of intensity I. Aperture of diameter $\dfrac{d}{2}$ in the central region of the lens is covered by a black paper. Focal length of lens and intensity of image now will be respectively
$\begin{aligned} & a)f\text{ and }\dfrac{I}{4} \\\ & b)\dfrac{3f}{4}\text{ and }\dfrac{I}{4} \\\ & c)f\text{ and }\dfrac{3I}{4} \\\ & d)f\text{ and }\dfrac{I}{2} \\\ \end{aligned}$

Answer 1

In the above diagram let us consider the lens to be very thin. If we take the rays of light from infinity, the rays will still pass through the lens from the half of the portion available and meet at the focus. The intensity of the image i.e. the brightness will reduce as the number of rays passing through the lens are obstructed by the black paper. The intensity of the rays forming the image is directly proportional to the amount of face area of the lens available. Hence we can calculate the intensity by determining the area available for the rays to pass.

Complete step by step answer:
To begin with let us first draw the ray diagram such that the aperture of the lens is covered at the centre.

If we see the above figure the rays pass through the focus in spite the centre portion of the lens being covered. The lens is very thin, therefore we can say that the marginal rays will hit the same point on the principle axis as that of some of the paraxial rays. Hence we can conclude that the focal length of the lens will not change.
Now let us understand how the intensity gets affected. One thing is for sure that the intensity will decrease as the amount of rays passing through the lens have decreased. It is given in the question that the lens is covered at the centre along the aperture of diameter $\dfrac{d}{2}$. Hence the radius of the circular region of the face area covered is $\dfrac{d}{4}$. The figure below shows this scenario.

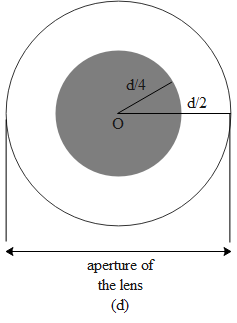
Let the face area of the above lens be ‘a’. Intensity of the image formed is proportional to the area available for the rays to pass i.e. $I\propto A$ where A is the area through which the rays of light pass. In the above diagram we can see that the area shaded white allows the rays to pass. Hence the area shaded white is equal to,
$\begin{aligned} & A=\pi {{\left( \dfrac{d}{2} \right)}^{2}}-\pi {{\left( \dfrac{d}{4} \right)}^{2}} \\\ & A=\pi \left( \dfrac{{{d}^{2}}}{4}-\dfrac{{{d}^{2}}}{16} \right) \\\ & A=\dfrac{3}{4}\pi {{\left( \dfrac{d}{2} \right)}^{2}}\text{the area of the lens }a=\pi {{\left( \dfrac{d}{2} \right)}^{2}} \\\ & A=\dfrac{3}{4}a \\\ \end{aligned}$
Let us say the intensity through the face area of the lens ‘a’ was $I$. Since $I\propto A$ the intensity across the lens now will be $\dfrac{3}{4}I$ . Hence we can conclude that the focal length of the lens does not change if we cover the lens but its intensity gets reduced i.e. to $\dfrac{3}{4}I$. Hence the correct option is c.

Note:
In the above question we have considered the lens to be very thin. If the lens is very thick then there will be spherical aberration in the lens. Therefore the marginal rays will suffer deviation and will form the image along a different point on the optical axis other than the focus. This is an important aspect in the above case as the centre of the lens is covered and most of the paraxial rays cannot meet the optical axis.