Question
Question: $\left( \frac{cos\theta + isin\theta}{sin\theta + icos\theta} \right)^4$...
(sinθ+icosθcosθ+isinθ)4
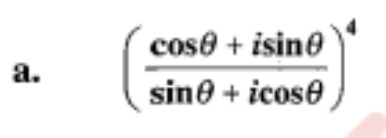
cos(8θ)+isin(8θ)
Solution
The problem asks us to simplify the given complex number expression: (sinθ+icosθcosθ+isinθ)4
We will simplify the expression inside the parenthesis first, then apply the power of 4.
Step 1: Express the numerator in polar form. The numerator is cosθ+isinθ. This is already in Euler's form: Numerator=eiθ
Step 2: Express the denominator in polar form. The denominator is sinθ+icosθ. We can use the trigonometric identities: sinθ=cos(2π−θ) cosθ=sin(2π−θ) Substituting these into the denominator: Denominator=cos(2π−θ)+isin(2π−θ) This is in Euler's form: Denominator=ei(2π−θ)
Step 3: Simplify the fraction inside the parenthesis. Let Z be the expression inside the parenthesis: Z=sinθ+icosθcosθ+isinθ=ei(2π−θ)eiθ Using the property eibeia=ei(a−b): Z=ei(θ−(2π−θ))=ei(θ−2π+θ)=ei(2θ−2π)
Step 4: Apply the power of 4 to the simplified fraction. The given expression is Z4: Z4=(ei(2θ−2π))4 Using De Moivre's Theorem, (eix)n=einx: Z4=ei⋅4(2θ−2π)=ei(8θ−2π)
Step 5: Convert the result back to trigonometric form and simplify. Using Euler's formula, eix=cosx+isinx: Z4=cos(8θ−2π)+isin(8θ−2π) Since cos(x−2π)=cosx and sin(x−2π)=sinx (due to the periodicity of trigonometric functions): Z4=cos(8θ)+isin(8θ)
The simplified expression is cos(8θ)+isin(8θ).
Explanation of the solution:
- Convert the numerator cosθ+isinθ to its Euler form eiθ.
- Convert the denominator sinθ+icosθ to its Euler form ei(2π−θ) by using sinθ=cos(2π−θ) and cosθ=sin(2π−θ).
- Divide the Euler forms: ei(2π−θ)eiθ=ei(θ−(2π−θ))=ei(2θ−2π).
- Raise the result to the power of 4 using De Moivre's theorem: (ei(2θ−2π))4=ei4(2θ−2π)=ei(8θ−2π).
- Convert back to trigonometric form: cos(8θ−2π)+isin(8θ−2π).
- Use the periodicity of cosine and sine functions (cos(x−2π)=cosx, sin(x−2π)=sinx) to get cos(8θ)+isin(8θ).
