Question

$A\left( {5,7} \right),B\left( {4,12} \right),C\left( {9,11} \right)$ and $D\left( {10,6} \right)$ are four points. Show that ABCD is a rhombus.

Answer 1

We can find the distance of AB using distance formula. We can also find the distances BC, CD and AD. Then by comparing the values we can prove that all the 4 sides are equal. Thus, we can prove that ABCD is a rhombus.

Complete step by step solution:
We are given that points A $\left( {5,7} \right)$ , B $\left( {4,12} \right)$ , C $\left( {9,11} \right)$ and D $\left( {10,6} \right)$.

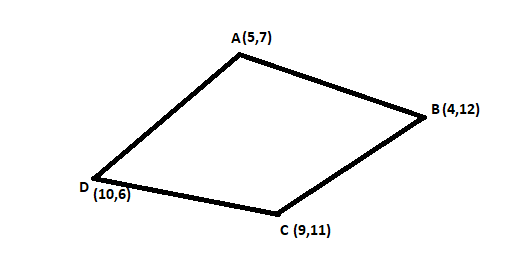
We know that distance between the points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by,
$d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}}$
So, the distance between the points A $\left( {5,7} \right)$ and B $\left( {4,12} \right)$ is
$AB = \sqrt {{{\left( {5 - 4} \right)}^2} + {{\left( {7 - 12} \right)}^2}}$
On simplification, we get
$\Rightarrow AB = \sqrt {{1^2} + {{\left( { - 5} \right)}^2}}$
On solving further, we have
$\Rightarrow AB = \sqrt {1 + 25}$
So, we have
$\Rightarrow AB = \sqrt {26}$ …. (1)
Now the distance between B $\left( {4,12} \right)$ and C $\left( {9,11} \right)$ is given by,
$\Rightarrow BC = \sqrt {{{\left( {4 - 9} \right)}^2} + {{\left( {12 - 11} \right)}^2}}$
On simplification, we get
$\Rightarrow BC = \sqrt {{{\left( { - 5} \right)}^2} + {1^2}}$
On solving further, we have
$\Rightarrow BC = \sqrt {25 + 1}$
So, we have
$\Rightarrow BC = \sqrt {26}$ … (2)
Now the distance CD is given by, C $\left( {9,11} \right)$ and D $\left( {10,6} \right)$.
$CD = \sqrt {{{\left( {9 - 10} \right)}^2} + {{\left( {11 - 6} \right)}^2}}$
On simplification, we get
$\Rightarrow CD = \sqrt {{{\left( { - 1} \right)}^2} + {5^2}}$
On solving further, we have
$\Rightarrow CD = \sqrt {1 + 25}$
So, we have
$\Rightarrow CD = \sqrt {26}$ … (3)
Now the distance between A $\left( {5,7} \right)$ and D $\left( {10,6} \right)$ is given by,
$AD = \sqrt {{{\left( {5 - 10} \right)}^2} + {{\left( {7 - 6} \right)}^2}}$
On simplification, we get
$\Rightarrow AD = \sqrt {{{\left( { - 5} \right)}^2} + {1^2}}$
On solving further, we have
$\Rightarrow AD = \sqrt {25 + 1}$
So, we have
$\Rightarrow AD = \sqrt {26}$ … (4)
From equations (1), (2), (3) and (4), we can say that
$\Rightarrow AB = BC = CD = AD = \sqrt {26}$
We know that a rhombus is a quadrilateral with all 4 sides equal. As all the sides are equal.

$\therefore$ ABCD is a rhombus.

Note:
Alternate method to solve this problem is given by,
We are given that points A $\left( {5,7} \right)$ , B $\left( {4,12} \right)$ , C $\left( {9,11} \right)$ and D $\left( {10,6} \right)$ .

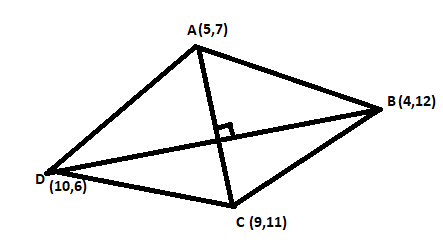
We know that for a rhombus, its diagonals are perpendicular.
We know that slope of the line joining the points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by,
$m = \dfrac{{{x_1} - {x_2}}}{{{y_1} - {y_2}}}$
So, the slope of the diagonal AC is,
$\Rightarrow {m_1} = \dfrac{{5 - 9}}{{7 - 11}}$
On simplification, we get
$\Rightarrow {m_1} = \dfrac{{ - 4}}{{ - 4}}$
Hence, we have
$\Rightarrow {m_1} = 1$
similarly, the slope of the diagonal BD is
$\Rightarrow {m_2} = \dfrac{{10 - 4}}{{6 - 12}}$
On simplification, we get
$\Rightarrow {m_2} = \dfrac{6}{{ - 6}}$
Hence, we have
$\Rightarrow {m_2} = - 1$
We know that if two lines are perpendicular, the product of their slope must be equal to -1.
$\Rightarrow {m_1} \times {m_2} = 1 \times - 1$
So, we have
$\Rightarrow {m_1} \times {m_2} = - 1$
Therefore, AC and BD are perpendicular. As the diagonals are perpendicular, we can say that ABCD is a rhombus.