Question

A leakage begins in the water tank at position P as shown in the figure. The initial gauge pressure at P was $5 \times {10^5}N/{m^2}$ .if the density of water is $1000kg/{m^3}$ the initial velocity with which water gushes out is:

A) $3.2m/\sec$
B) $32m/\sec$
C) $28m/\sec$
D) $2.8m/\sec$

Answer 1

To solve this question we use Bernoulli’s theorem which is ${P_1} + \dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} = {P_2} + \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2}$
And we know the gauge pressure is pressure above that of the atmospheric pressure at that point can be represented as $P - {P_{atm}} = \rho gh$ .
Where $P \Rightarrow$ is the total pressure at that point or at that level

Step by step solution:
First we mark another point Q at the same level of P let as assume the point P and Q are $h$ height below the free surface of the water tank.
As shown in figure.

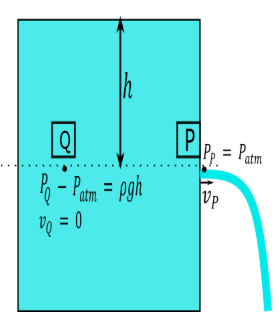
From figure we can write the gauge pressure at point Q is ${P_Q} - {P_{atm}} = \rho gh$
Where $\rho \Rightarrow$ density of water
${P_Q} \Rightarrow$ Total pressure at point Q
$h \Rightarrow$ Height from free surface
So from this we can Wright the pressure at point Q is
$\Rightarrow {P_Q} = {P_{atm}} + \rho gh$ ......... (1)
Pressure at point P is equal to the atmospheric pressure
${P_P} = {P_{atm}}$ ......... (2)
Velocity at point Q is approximately equal to zero
${v_Q} = 0$....... (3)
Let us assume the velocity at point P is with which water comes out is ${v_P}$
Step 2
Now we apply Bernoulli’s theorem for horizontal points P and Q.
$\Rightarrow {P_P} + \dfrac{1}{2}\rho {v_P}^2 + \rho g{h_P} = {P_Q} + \dfrac{1}{2}\rho {v_Q}^2 + \rho g{h_Q}$
Because point P and Q are at same horizontal level ${h_P} = {h_Q}$ so Bernoulli theorem reduced to
$\Rightarrow {P_P} + \dfrac{1}{2}\rho {v_P}^2 = {P_Q} + \dfrac{1}{2}\rho {v_Q}^2$
Put all values in this equation from (1) (2) and (3)
$\Rightarrow {P_{atm}} + \dfrac{1}{2}\rho {v_P}^2 = \left( {{P_{atm}} + \rho gh} \right) + \dfrac{1}{2}\rho {\left( 0 \right)^2}$
$\Rightarrow \dfrac{1}{2}\rho {v_P}^2 = \rho gh$
Now ${P_Q} - {P_{atm}} = \rho gh = 5 \times {10^5}N/{m^2}$ given in question
Put $\rho gh = 5 \times {10^5}$ and density of water $\rho = 1000kg/{m^3}$
$\Rightarrow \dfrac{1}{2} \times 1000 \times {v_P}^2 = 5 \times {10^5}$
$\Rightarrow {v_P}^2 = \dfrac{{5 \times {{10}^5} \times 2}}{{1000}}$
Further solving
$\Rightarrow {v_P} = \sqrt {\dfrac{{5 \times {{10}^5} \times 2}}{{1000}}}$
$\Rightarrow {v_P} = \sqrt {1000}$
$\Rightarrow {v_P} = 31.62m/\sec$
Hence the velocity to exit the water tank at point P is approximately $32m/\sec$

therefore Option B is correct

Note:
We can solve this question by another short method which is given below
We know gauge pressure $P = \rho gh$ from this we can find height of hole from free surface
$\Rightarrow 5 \times {10^5} = 1000 \times 10 \times h \\\ \Rightarrow h = 50m \\\$
And now apply Torricelli’s theorem formula velocity of Efflux $v = \sqrt {2gh}$
$\Rightarrow v = \sqrt {2 \times 10 \times 50} \\\ \Rightarrow v = \sqrt {1000} \\\ \therefore v = 31.62m/\sec \\\$