Question
Question: A layer of oil with density \(724\text{ kg/}{{\text{m}}^{3}}\) floats on water of density \(1000\tex...
A layer of oil with density 724 kg/m3 floats on water of density 1000 kg/m3. A block floats at the oil water interface with 61 of its volume in oil and 65 of its volume in water as shown in the figure. What is the density of the block?
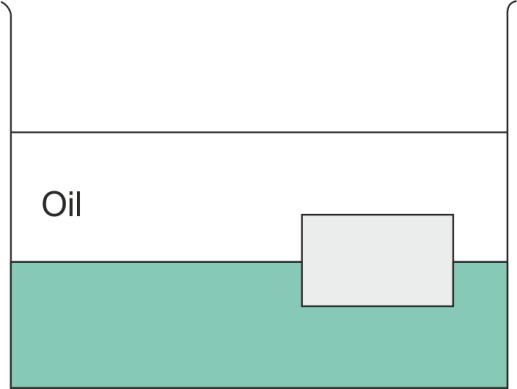
(A) 1024 kg/m3
(B) 1276 kg/m3
(C) 776 kg/m3
(D) 951 kg/m3
Solution
Oil molecules are only attracted to other oil molecules. Water is more dense than oil; they can’t mix oil floats above the water. Density is the weight of a substance for a specific volume.
Density=volumemass, volume×density=mass
Formula used:
By using Archimedes Principle
Upthrust = Weight of the liquid displaced.
(VPb)g=(Voρ1)g+(VWρ2)g
(VPb)g→Volume of block ×density of block × specific gravity.
g→specific gravity
V0→ Volume of oil.
ρ1→ Density of oil
Vw→ Volume of water
ρ2→ Density of water
Complete solution:
Given data:
Density of oil ρ1=724 kg/m3
Density of water ρ2=1000 kg/m3
According to Archimedes principle
Upthrust = Weight of liquid displaced
(Vρ)bg=V0ρ1g+Vwρ2g
⇒(Vρ)bg=6V(724)g+65V(1000)g
Where, Vb→ block volume, ρb→ density of block
V0=6V,V∞=65V
⇒(Vρ)bg=(6724V+65000V)g
(Vρ)b=6724V+65000V
Vρb=65724V
ρb=65724
ρb=954 kg/m3
Therefore the density of the block is 954 kg/m3 i.e. option (d) is correct.
Additional information:
Density of liquid water is 1 g/cm3 and vegetable oil is 0.93 g/cm3. Ice has a density of 0.92 g/cm3 Which is why it floats on water and oil.
Note:
Oil is less dense than water. The molecules that make the oil are larger than those that make up water, so they cannot pick as tightly together as the water molecules.
