Question

A lateral edge of a regular rectangular pyramid is a cm long. The lateral edge makes an angle $\alpha$ with the plane of the base. For what $\alpha$ is the volume of the pyramid the greatest?

Answer 1

Hint : In this question, we need to evaluate the value of $\alpha$ at which the volume of the pyramid is the greatest such that the lateral edge makes an angle $\alpha$ with the plane of the base. To solve this type of question, find the volume of the pyramid in terms of angle α and then equate the first derivative of the volume of the pyramid to zero and make sure the second derivative should be less than zero.

Complete step-by-step answer :
Given that there is a regular rectangular pyramid whose lateral edge makes an angle α with the plane base.

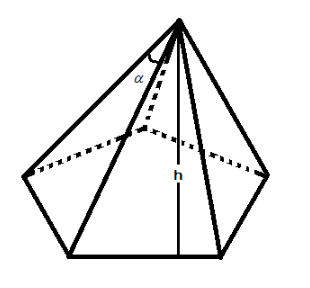
We have to find the value of α for which the volume of the regular rectangular pyramid has the greatest volume.
Suppose l, b, and h are the length breadth and the height if the regular rectangular pyramid
So, the Volume of rectangular pyramid is given as:
$V = \dfrac{{lbh}}{3}$
Now applying the trigonometric ratio property, we get

$$sin\alpha = \dfrac{h}{a} \\\ \Rightarrow h = asin\alpha \;$$

And, $l = b = 2a$
On putting the above values of length breadth and height, we get,
$V = \dfrac{{4{a^3}sin\alpha }}{3}$
Now find the first derivative of the volume with respect to $\alpha$, we get
$\dfrac{{dV}}{{d\alpha }} = \dfrac{{4{a^3}cos\alpha }}{3}$
For maxima, the second derivative should be less than zero. So, the second derivative is

$$\dfrac{{{d^2}V}}{{d{\alpha ^2}}} = - \dfrac{{4{a^3}sin\alpha }}{3} \\\ \Rightarrow \dfrac{{{d^2}V}}{{d{\alpha ^2}}} < 0 \;$$

Which fulfills the criteria of maximum.
Now equate the first derivative of volume to zero and find the value α
∴

$$\dfrac{{dV}}{{d\alpha }} = 0 \\\ \Rightarrow \dfrac{{4{a^3}cos\alpha }}{3} = 0 \\\ \Rightarrow 4{a^3}cos\alpha = 0 \;$$

Here
$4{a^3} \ne 0\;$ then,
$cos\alpha = 0$
We know $cos\alpha$ can be zero when
$\therefore \alpha = \dfrac{\pi }{2}\;or\;\dfrac{{3\pi }}{4}$
Hence, for $\alpha = \dfrac{\pi }{2}\;or\;\dfrac{{3\pi }}{4}$ , the volume of regular rectangular pyramid will be greatest.
So, the correct answer is “ $\alpha = \dfrac{\pi }{2}\;or\;\dfrac{{3\pi }}{4}$ ”.

Note : It is worth noting down here that the all the slant height of the regular pyramid will make an angle of $\alpha$ with the base of the pyramid. Here, $cos\alpha = 0$ can be zero for n values of $\alpha$ but we have taken only two values because for a regular rectangular pyramid $\alpha$ can vary from 0 to $\pi$ only.