Question

A large wooden raft is flowing with a river stream. A man on the raft dives into the river and swims down the stream for 15 minutes and then he turns about and comes back to the raft. The swimming speed of man is 5km/h in still water and the speed of the river is 4km/h. The distance moved by the raft till the man comes back to raft is
A. 1 km
B. 2 km
C. 3 km
D. 4 km

Answer 1

First, calculate the speeds of the man when he swims upstream and downstream. Find the displacement of the raft in 15 minutes. Also, calculate the distance moved by the man in those 15 minutes. Then find the distance moved by the raft until the man reaches the raft. Then add the two distances of the raft.

Formula used: $\text{distance = speed }\\!\\!\times\\!\\!\text{ time}$

Complete step by step answer:
It is given that the speed of the river is 4 km/h. This means that the speed of the raft will be 4km/h (because the raft will be moving with the flow of the river). The speed of the raft will be 4 km/h throughout the case.
It is given that the swimming speed of the man is 5 km/h in still water. When the man swims down the stream (along with flow of the water), the flow of the river will assist him and his speed will increase to $5+4=9km/h$.
And when the man swims up the stream (against the flow of the water), the flow of the river opposes his motion and his speed will reduce to $5-4=1km/h$.
It said that the man jumped from the raft and swam down the stream for 15 minutes. In this time the raft will move by a distance of ${{d}_{1}}=4km{{h}^{-1}}\times 15\min =4km{{h}^{-1}}\times 15\left( \dfrac{1}{60}h \right)=1km$ (by using $\text{distance = speed }\\!\\!\times\\!\\!\text{ time}$). This displacement is along the flow of the river.
And the distance moved by the man in this time is ${{d}_{m}}=9km{{h}^{-1}}\times 15\left( \dfrac{1}{60}h \right)=2.25km$.

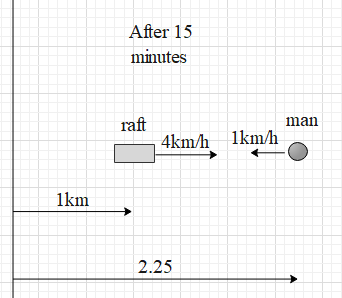
Therefore, the distance between the man and the raft after 15 minutes is ${{d}_{m}}-{{d}_{1}}=2.25-1=1.25km$.
After 15 minutes, it is said that the man turns back and swims to the raft (i.e. upstream). Since the man is swimming upstream, his speed will be 1 km/h.
After 15 minutes, let the distance moved by the raft be x. This means that the distance moved by the man until he reaches the raft is 1.25 – x.
And let the time taken for the man to reach the raft be t.
Therefore, by using $\text{distance = speed }\\!\\!\times\\!\\!\text{ time}$ we can write that
$x=4t$ ….. (i)
And
$1.25-x=t$
Substitute the value of t in (i).
$\Rightarrow x=4(1.25-x)$
$\Rightarrow x=5-4x$
$\Rightarrow x=1km$.
Therefore, the total distance moved by the raft until the man returns to it is ${{d}_{1}}+x=1+1=2km$.

So, the correct answer is “Option B”.

Note: We can also use relative motion to find the distance moved by the raft. We can analyse the situation with respect to the raft.
When we analyse the situation with respect to the raft, it means that the raft is at rest and all other motion is seen in its respect. The raft is moving with a constant speed of 4km/h along with the flow of the river. Therefore, when the man is actually moving downstream with a speed of 9km/h, his speed with the raft is 9 – 4 = 5km/h.
And when the man is swimming upstream with an actual speed of 1km/h, his speed with respect to the raft is 1 + 4 = 5km/h.
Since the raft is at rest, the man has to cover the same distance while swimming upstream and downstream. And we found that the speeds are the same in both conditions. Therefore, the time taken in swimming upstream and downstream will be equal. This means that the man takes 15 minutes to reach the raft after he turns back.
Therefore, the total time taken for the man to return to the raft is 15 + 15 = 30 minutes.
In 30 minutes, the raft will move by a distance of $4km{{h}^{-1}}\times 30\min =4km{{h}^{-1}}\times 30\left( \dfrac{1}{60}h \right)=2km$.