Question

A large open tank has two holes in the wall. One is a square hole of side $L$ at a depth $y$ from the top and the other is a circular hole of radius $R$ at a depth $4y$ from the top. When the tank is completely filled with water, the quantities of water flowing out per second from the two holes are the same. Then value of R is:
A. $\dfrac{L}{{\sqrt {2\pi } }}$
B. $2\pi L$
C. $L\sqrt {\dfrac{2}{\pi }}$
D. $\dfrac{L}{{2\pi }}$

Answer 1

First find the velocity of water through the square and the circular hole; use the formula of velocity of efflux. Find the rate of flow through both the holes. It is given that the rate of flow of both the holes are the same, so equate the values obtained to find the value of radius of the circular hole.

Complete step by step answer:
Given, the tank has two holes. One is a square hole of side $L$ which is at a depth $y$ from the top and one circular hole of radius $R$ at a depth $4y$ from the top. We draw a diagram to visualize the problem.

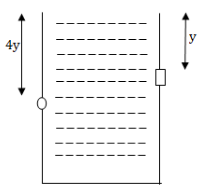
At first, we find the velocity of water through the square and the circular hole.
Let ${v_s}$ be the velocity of water through the square and ${v_c}$ be the velocity of water through the circular hole.

We now use the formula of velocity of efflux to find the velocity through the holes.
Velocity of efflux can be defined as the velocity acquired by an object upon falling from rest through a height h and it written as,
$v = \sqrt {2gh}$
$g$ is the acceleration due to gravity and $h$ is the height.
Now, for square hole, the height is $y$, so using the formula of velocity of efflux we get velocity of water falling through square hole as,
${v_s} = \sqrt {2gy}$ (i)
And for circular hole, the height is $4y$, so using the formula of velocity of efflux we get velocity of water falling through circular hole as,

\Rightarrow {v_c} = 2\sqrt {2gy} $$ (ii) Rate of flow is given, $$AV$$ where $$A$$is the area of the aperture and $$V$$ is the velocity of the liquid. Rate of flow of water through square hole will be, $${R_s} = {A_1}{v_s}$$ The square is of side $$L$$ so the area of the square hole will be $${L^2}$$ , putting the value area and value of velocity from equation (i) in above equation, we get $${R_s} = {L^2}\sqrt {2gy} $$ Similarly, rate of flow of water through circular hole will be, $${R_c} = {A_2}{v_c}$$ The radius of the circular hole is $$R$$ so the area will be$$\pi {R^2}$$. Putting the value of area and value of velocity from equation (ii), we have $${R_c} = \pi {R^2}\sqrt {2g4y} $$ It is given the rate of flow of water from both the holes are same, that is $${R_c} = {R_s}$$ Now, putting the values of $${R_c}$$ and $${R_s}$$ we get $$\pi {R^2}\sqrt {2g4y} = {L^2}\sqrt {2gy} $$ $$\Rightarrow 2\pi {R^2}\sqrt {2gy} = {L^2}\sqrt {2gy} \\\ \Rightarrow 2\pi {R^2} = {L^2} \\\ \Rightarrow {R^2} = \dfrac{{{L^2}}}{{2\pi }} \\\ \therefore R = \dfrac{L}{{\sqrt {2\pi } }} $$ Therefore, the radius of the circular hole is $$\dfrac{L}{{\sqrt {2\pi } }}$$. **Hence, the correct answer is option A.** **Note:** Here, the depth of the hole from the top was given. But if any such question height from the bottom is given then first calculate its depth from the top and then go for the calculation using velocity of efflux. Students sometimes make such mistakes, so always read carefully the given conditions and before applying any formula always check whether the quantities in the formula are the same as the given quantities.